Moto parabolico di un proiettile
Esercizio sul moto parabolico di un proiettile
Un cacciatore che si trova sulla cima di una montagna spara orizzontalmente un proiettile che segue una traiettoria parabolica di equazione:
y = 4,9 · 10-4 · x2 / 4
in cui l'asse x è rivolto nello stesso verso della velocità e l'asse y è rivolto verso il basso, con l'origine coincidente col proiettile quando è ancora fermo.
Calcolare le componenti x e y della velocità dopo 20 s ed il modulo della velocità risultante sempre per t = 20 s.
Svolgimento
L'esercizio propone di considerare un moto parabolico di tipo orizzontale, cioè con componente nulla della velocità verticale iniziale, a partire dalla conoscenza dell'equazione della parabola che è traiettoria del moto.
Iniziamo col disegnare la situazione e a porre correttamente il sistema di riferimento cartesiano:
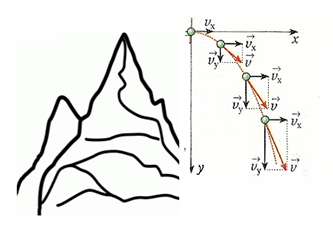
Come vediamo dalla figura, all'inizio il punto ha solo componente orizzontale della velocità.
Man mano che scende però accanto alla componente orizzontale, che rimane costante lungo tutta la discesa, compare il termine relativo alla velocità verticale Vy che aumenterà in quanto si tratta di moto rettilineo uniformemente accelerato con accelerazione pari a g.
Scriviamo le equazioni che descrivono il moto del proiettile durante la sua caduta lungo x e lungo y:
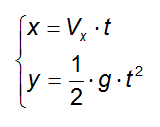
Ricaviamo t dalla prima equazione:
t = x / Vx
e sostituiamolo nella seconda:
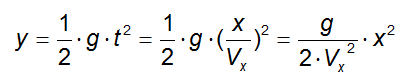
Confrontiamo ora tale generica equazione con l'equazione data:
y = 4,9 · 10-4 · x2 / 4
Dal confronto emerge che:
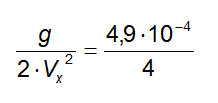
Essendo g = 9,8 m/s2 allora:
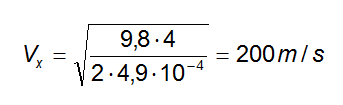
che risulta essere la velocità orizzontale iniziale con cui viene sparato il proiettile e che, come già detto, si mantiene costante durante la caduta, e dunque anche al tempo t = 20 s.
Per ricavare invece il valore della velocità verticale, ricordiamo la legge che lega velocità e tempo in un moto rettilineo uniformemente accelerato:
Vy = g · t + Voy
Ora essendo la velocità iniziale verticale nulla, avremo che:
Vy = g · t
e per t = 20 s:
Vy (20) = 9,8 · 20 = 196 m/s
Il modulo della velocità risultante V dopo 20 s sarà, per la regola del parallelogramma la diagonale del rettangolo che ha per lati Vx e Vy:
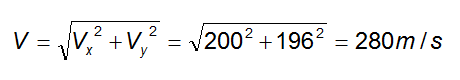
In definitiva dopo 20 s le componenti x e y della velocità sono 200 m/s e 196 m/s, mentre il modulo della velocità risultante sarà pari a 280 m/s.
Link correlati:
Quali sono le formule sul moto parabolico?
Studia con noi