Lavoro compiuto dalla Forza di Lorentz
Calcolo del lavoro compiuto dalla Forza di Lorentz
Un conduttore rettilineo lungo mezzo metro si muove all'interno di un campo magnetico di intensità 10-4 T con velocità costante e perpendicolare alle linee di forza del campo.
Attraverso un voltmetro si misura ai capi del conduttore una ddp indotta di 0,20 V.
Calcolare la velocità del conduttore attraverso il campo e quanto vale il lavoro compiuto dalla Forza di Lorentz su un singolo elettrone di conduzione.
Svolgimento
La situazione descritta nel problema corrisponde a quella relativa ad una regione di spazio in cui è presente un campo magnetico attraverso il quale si sta muovendo a velocità costante V una barretta conduttrice lunga L.
La velocità V risulta perpendicolare al campo, per cui ipotizziamo che il campo sia entrante nel foglio e la velocità rivolta verso destra:
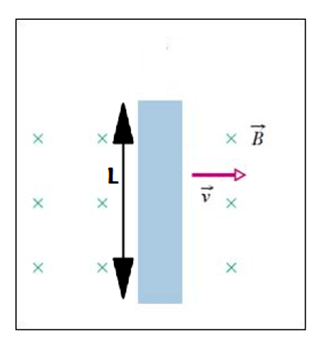
In questo problema la scelta di campo entrante o uscente è arbitraria così come il verso della velocità.
Attraverso la barretta il flusso del campo magnetico varierà nel tempo, in quanto il conduttore si sta muovendo, e tale variazione per la legge di Faraday-Neumann provoca una corrente indotta. E se è presente una corrente, sarà anche presente una tensione indotta ai capi del conduttore:
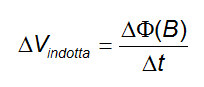
Ricordando che il flusso del campo magnetico è definito come:
Φ(B) = S · B · cosα
in cui
- S è la superficie di cui si deve calcolare il flusso del campo;
- B è l'intensità del campo magnetico;
- α è l'angolo che la direzione di B forma con la direzione perpendicolare alla superficie.
Avremo che:
L = 0,5 m
α = 0°
B = 10-1 T
ΔVind = 0,20 V
Dunque sostituiamo nella formula della ΔVind la formula che ci consente di calcolare la variazione del flusso:
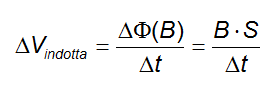
Ora la superficie attraverso la quale bisogna calcolare il flusso è quella che la barretta crea col suo movimento verso destra, dalla posizione 1 alla 2, e vale il prodotto della lunghezza del conduttore per la distanza orizzontale d percorsa:
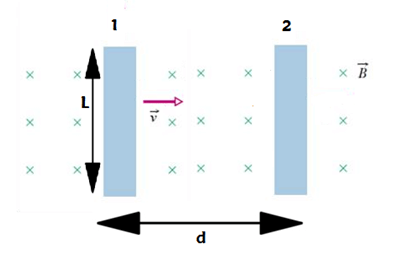
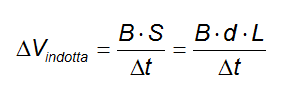
Ma il rapporto tra d e la variazione di tempo non rappresenta altro che la velocità con cui la barretta si sta muovendo all'interno del campo:
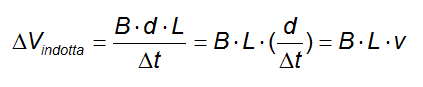
Dalla precedente possiamo dunque ricavare il valore della velocità v:
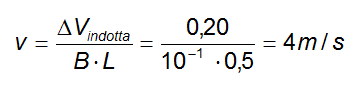
Il problema chiede infine di determinare il lavoro che la Forza di Lorentz compie su ogni singolo elettrone di conduzione.
Ricordando che il lavoro svolto su una carica vale:
L = q · ΔV
e che un elettrone ha carica pari a:
q = 1,6·10-19 C
otteniamo:
L = 1,6·10-19 · 0,2 = 0,32 ·10-19 J = 0,20 eV
Dunque in definitiva la velocità con cui il conduttore si sta muovendo all'interno del campo magnetico vale 4 m/s e il lavoro svolto sugli elettroni di conduzione vale 0,20 eV (0,20 elettronvolt).
Studia con noi