Velocità tangenziale
Che cos'è la velocità tangenziale?
Il vettore velocità tangenziale è il vettore che rappresenta la velocità con cui si muove un punto lungo una circonferenza.
Esso ha la direzione della tangente alla traiettoria nella posizione che il punto occupa in quell'istante, cioè perpendicolare al raggio della traiettoria circolare che passa per quel punto.
Il verso è orario o antiorario a seconda di come si sta muovendo il punto sulla circonferenza.
Nella figura seguente sono rappresentate diverse posizioni assunte dal punto lungo la sua rotazione e per ogni posizione assunta è stato disegnato il vettore tangente che ne rappresenta la velocità tangenziale.
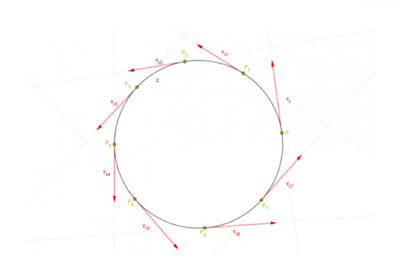
Velocità tangenziale nel moto circolare uniforme.
Velocità tangenziale nel moto circolare uniforme
Se il modulo della velocità tangenziale rimane sempre costante allora si parla di moto circolare uniforme.
In questo caso solo il modulo della velocità rimane costante, invece cambia istante per istante la direzione.
Detti R il raggio della traiettoria circolare e T il periodo del moto, la velocità tangenziale V si calcola come il rapporto tra lo spazio percorso ed il tempo impiegato a percorrere tale spazio.
Ricordando che la lunghezza di una circonferenza è data da 2·π·R e che il tempo impiegato a compiere un giro completo è proprio il periodo T allora:
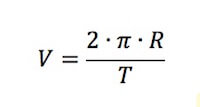
Sfruttando la relazione tra periodo e frequenza:
V = 2 · π · R · f
La velocità tangenziale si misura in m/s.
Introducendo il concetto di velocità angolare :
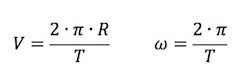
le due formule possono essere legate tra di loro attraverso la seguente espressione:
V = ω · R
da cui
ω = V / R
Velocità tangenziale ed accelerazione nel moto circolare
In un moto circolare uniforme il vettore velocità tangenziale mantiene costante il proprio modulo lungo tutto la circonferenza, pertanto il corpo percorre archi uguali in tempi uguali.
Visto che però la direzione della velocità cambia istante per istante è necessario introdurre il concetto di accelerazione centripeta, che interviene nella variazione di direzione del vettore velocità.
L'accelerazione centripeta è un vettore perpendicolare alla velocità e diretta verso il centro lungo la direzione del raggio:
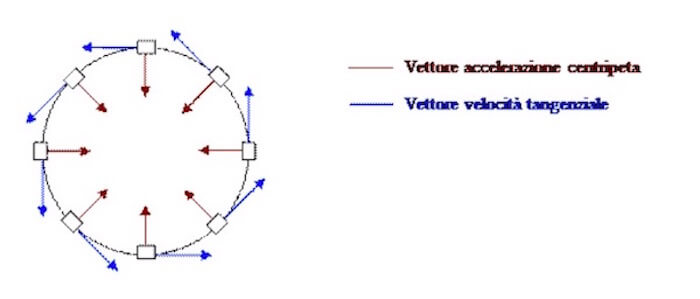
Se il moto circolare non è uniforme ma il modulo del vettore velocità tangenziale cambia nel tempo allora si parlerà di accelerazione tangenziale, che ha la stessa direzione del vettore velocità:
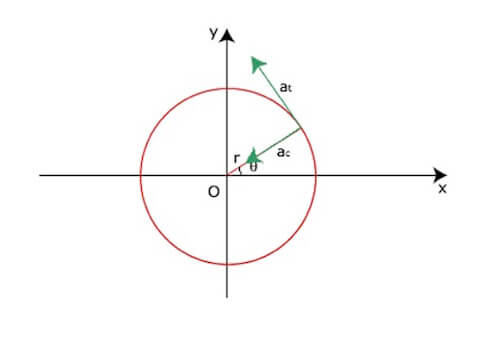
Nella figura sono rappresentati i due vettori accelerazione centripeta e tangenziale; si può notare come essi siano perpendicolari tra di loro.
La risultante dei due vettori sarà il vettore a diretto in una direzione diversa rispetto ad ac ed at.
Nel moto circolare uniforme invece essendo at = 0 (velocità tangenziale costante) l'unica accelerazione presente è quella centripeta.
L'accelerazione centripeta è data dal rapporto tra il quadrato della velocità tangenziale e il raggio della circonferenza.
In un moto circolare uniforme l'accelerazione centripeta rimane costante.
ac = v2 / r
Velocità tangenziale nel moto circolare uniformemente accelerato
Nel moto circolare uniformemente accelerato il vettore velocità tangenziale non ha più modulo costante, questo vuol dire che il punto materiale sta ruotando incrementando (o decrementando) la propria velocità.
Il punto sarà dunque soggetto ad un'accelerazione tangenziale costante (perché; il moto è di tipo uniforme) che ha lo stesso verso della velocità.
Il raggio vettore spazzerà a sua volta con velocità angolare sempre crescente (o decrescente) l'angolo al centro, allora si parla di accelerazione angolare solitamente indicata con α.
Visto che l'accelerazione tangenziale è costante anche l'accelerazione angolare è costante e accelerazione angolare media e istantanea coincidono:
α = Δω / Δt
ed ha come unità di misura i rad/s2.
Le leggi del moto circolare uniformemente accelerato sono molto simili a quelle del moto rettilineo uniformemente accelerato con la differenza che qui si considera un'accelerazione angolare α, un angolo iniziale θ0 e finale θ ed una velocità angolare iniziale ω0 e finale ω:
ω = ω0 + α · t
θ = ½ · α · t2 + ω0 · t + θ0
2 · α · (θ - θ0) = ω2 - ω02
Esercizio sulla velocità tangenziale
Calcolare Il modulo della velocità tangenziale della Terra nel suo moto di rivoluzione attorno al Sole sapendo che il raggio della sua orbita attorno all'astro è pari a 1,49 · 1011 m.
Lo svolgimento dell'esercizio lo trovi qui: velocità tangenziale della Terra.
Altro esercizio
Nelle tre figure sotto sono rappresentate tre situazioni temporali diverse legate al moto di una particella che si sta muovendo in senso antiorario lungo una traiettoria circolare.
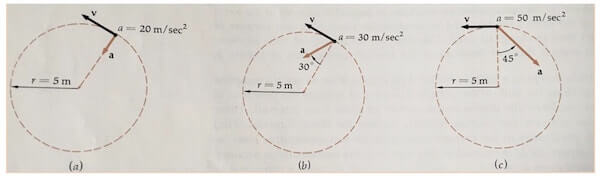
Calcolare il valore della velocità tangenziale per ogni caso.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della velocità tangenziale nel moto circolare.
Studia con noi