Principio di sovrapposizione delle onde
Spiegazione ed enunciato del principio di sovrapposizione delle onde
Enunciato del principio di sovrapposizione: se due o più onde della stessa natura (onde elettromagnetiche, onde sonore) che si propagano nello stesso mezzo si sovrappongono in un certo punto dello spazio allora la perturbazione generata è pari alla somma algebrica delle oscillazioni di ciascuna onda presa singolarmente.
Spiegazione del principio di sovrapposizione delle onde
Grazie al principio di sovrapposizione possiamo capire perché possiamo ad esempio sentire i suoni distinti di diversi strumenti provenienti da un'orchestra senza che essi si perturbino a vicenda. L'effetto di ciascuna perturbazione rimane lo stesso di quello che si avrebbe se ciascun'onda si propagasse singolarmente.
Grazie a tale principio possiamo capire anche perché se due fasi di luce laser si incontrano poi proseguono tranquillamente il loro percorso senza essere alterati dall'incontro con l'altro fascio.
Il principio di sovrapposizione vale per qualsiasi onda sia meccanica sia elettromagnetica sia in un mezzo sia nel vuoto.
Serie di Fourier
Il principio di sovrapposizione può anche essere dedotto da un teorema matematico scritto da Fourier per cui qualsiasi onda può essere vista come composizione e somma di onde armoniche semplici:
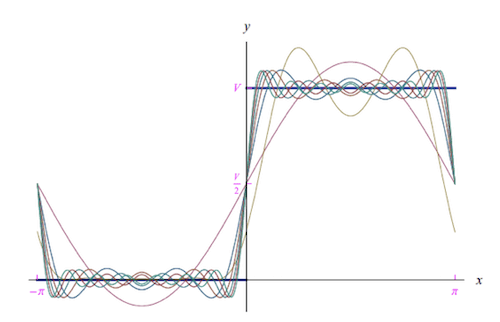
Serie di Fourier.
Interferenza costuttiva e distruttiva
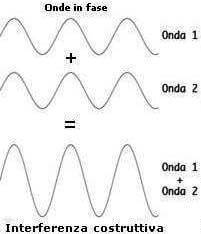
Il fenomeno dell'interferenza si ha quando due onde che si sovrappongono in un certo punto dello spazio si rafforzano oppure si indeboliscono a vicenda.
Consideriamo due onde armoniche che si propagano alla stessa frequenza e nello stesso verso.
Le due onde possono essere descritte dall'equazioni in funzioni del tempo:
y1 = a ∙ cos(ω ∙ t)
e
y2 = a ∙ cos(ω ∙t + φ0)
le due onde sono anche caratterizzate dalla stessa ampiezza ma la seconda onda ha una fase diversa rispetto alla prima (la cui fase è nulla).
Si dimostra che l'onda che si crea dalla sovrapposizione delle due iniziali ha equazione:
y = A ∙ cos[ω ∙ t + (φ0/2)]
con ampiezza A pari a:
A = 2 ∙ a ∙ cos(φ0/2)
Se la differenza di fase tra le due onde, ovvero la differenza di fase della seconda onda (essendo la prima nulla) è pari a:
φ0 = (2 ∙ k + 1) ∙ π (con k numero intero positivo o negativo)
allora il coseno di φ0/2 è pari a:
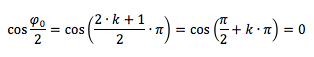
Per cui A = 0 le due onde si annullano → interferenza distruttiva
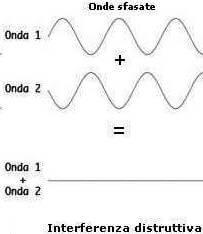
Se invece la fase iniziale della seconda onda è pari a:
φ0 =2 ∙ k ∙ π (con k numero intero positivo o negativo)
allora il coseno di φ0/2 è pari a
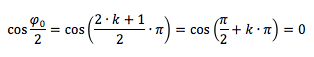
Per cui l'ampiezza dell'onda risultante raddoppia → interferenza costruttiva
Esercizio #1
Due onde armoniche che procedono in un mezzo con la stessa frequenza e la stessa ampiezza (ampiezza = a), interferiscono tra di loro e generando un'onda risultante la cui ampiezza è la metà di ciascuna ampiezza delle onde originarie.
Determinare lo sfasamento tra le due onde.
Lo svolgimento dell'esercizio lo trovi qui: differenza di fase tra due onde.
Esercizio #2
Due onde armoniche sono descritte dalle seguenti equazioni:
y1 = 0,4 ∙ cos(20 ∙ π ∙ t)
e
y2 = 0,4 ∙ cos[20 ∙ π ∙ t + (π/3)]
Se le due onde si vengono a trovare nello stesso punto, determinare l'equazione dell'onda risultante.
Lo svolgimento dell'esercizio lo trovi qui: interferenza di due onde armoniche.
Studia con noi