Gittata ed altezza massima nel moto parabolico
Come si calcolano la gittata e l'altezza massima nel moto parabolico
Definiamo "proiettile" un corpo puntiforme, che viene lanciato in aria con una velocità iniziale che abbia almeno una componente orizzontale.
Il movimento del proiettile non è altro che la somma di due moti: un moto rettilineo uniforme lungo l'asse x ed un moto rettilineo uniformemente accelerato lungo l'asse y.
Per il principio di composizione dei movimenti nasce il moto parabolico.
Al proiettile viene inizialmente impressa una velocità iniziale di modulo V0 che può essere inclinata di un angolo α rispetto all'orizzontale o essere orizzontale (se il moto parte da una certa altezza).
Per cui il vettore velocità iniziale ha due componenti x e y:
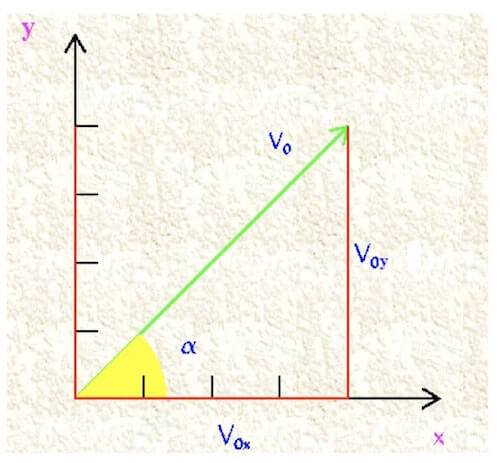
Chiamiamo queste due componenti V0x e V0y e il loro valore è pari a:
V0x = V0 ∙ cosα
V0y = V0 ∙ senα
Lungo l'asse x, come detto, il proiettile procede di moto rettilineo uniforme con velocità pari a V0x che rimarrà tale fino a che il proiettile si arresta toccando terra.
Lungo l'asse y invece il proiettile procede di moto rettilineo uniformemente accelerato.
Pertanto, detti V0 il modulo della velocità iniziale ed α l'angolo che essa forma con l'asse x, le due leggi orarie lungo i piani X e Y saranno del tipo:
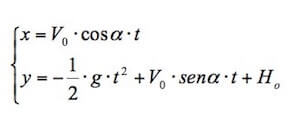
In cui (V0 ∙ cosα) e (V0 ∙ senα) sono rispettivamente le componenti orizzontali e verticali della velocità, mentre H0 è l'eventuale altezza iniziale da cui parte il moto.
Sviluppando il sistema si ottiene l'equazione della parabola, traiettoria del moto, con y espressa in funzione di x, senza tener conto del tempo.
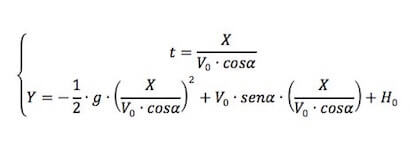
Sviluppando la seconda:
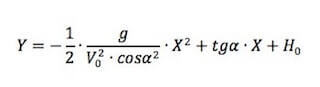
Che è appunto l'equazione di una parabola con la concavità rivolta verso il basso (coefficiente di X2 è minore di zero).
Calcolo della gittata nel moto parabolico
Si definisce gittata la distanza orizzontale tra il punto di lancio e quello di caduta al suolo.
Questo punto della traiettoria del proiettile corrisponde al momento in cui la coordinata Y = 0, ovvero il corpo tocca il suolo.
Se il corpo parte dal suolo (H0 = 0) imponendo Y = 0 nell'equazione della traiettoria otterremo:
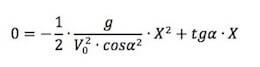
Raccogliamo X:
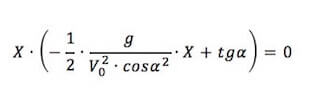
La precedente si annulla per X = 0 (situazione iniziale) e per:
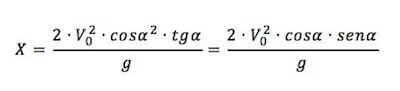
in cui abbiamo sostituto il valore della tangente dell'angolo con la sua definizione:
tgα = senα/cosα
La gittata indicata con la lettera G è dunque calcolabile come:
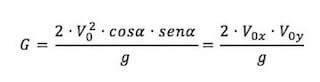
In cui V0 è il modulo della velocità iniziale mentre V0x e V0y sono rispettivamente la sua componente orizzontale e verticale iniziale.
Calcolo della altezza massima nel moto parabolico
Allo stesso modo è possibile calcolare l'altezza massima raggiunta dal corpo intesa geometricamente come l'ordinata del vertice della parabola e numericamente pari a:
Hmax = (V0 ∙ senα)2 / (2 ∙ g)
Esercizio
Un proiettile viene sparato dalla sommità di una torre alta 25 m con una velocità orizzontale pari a 200 m/s.
Calcolare la gittata e la velocità con cui il proiettile toccherà il suolo.
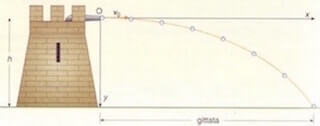
Lo svolgimento dell'esercizio lo trovi qui: esercizio sul calcolo della gittata.
Esercizi sul moto parabolico
Se ti interessano li puoi trovare qui: esercizi sul moto parabolico.
Link correlati:
Quali sono le formule sul moto parabolico?
Studia con noi