Esercizio sul calcolo della gittata
Esercizio sul calcolo della gittata nel moto parabolico
Un proiettile viene sparato dalla sommità di una torre alta 25 m con una velocità orizzontale pari a 200 m/s.
Calcolare la gittata e la velocità con cui il proiettile toccherà il suolo.
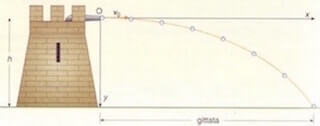
Svolgimento dell'esercizio
Si tratta di un moto parabolico di tipo orizzontale in quanto il proiettile parte dal vertice della parabola che sarà la traiettoria del proiettile.
L'intero percorso rappresenta dunque metà di una parabola intera.
Il procedimento è lo stesso per un moto parabolico tradizionale considerando che l'angolo di lancio iniziale però è di α = 0°pertanto la velocità iniziale non ha alcuna componente verticale (infatti sen0 = 0).
I dati forniti sono:
Vox = 200 m/s
H0 = 25 m
Scriviamo le equazioni che descrivono il moto del proiettile durante la sua caduta:
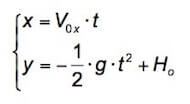
in cui Ho è l'altezza della torre.
Nel nostro riferimento l'asse y è rivolto verso l'alto ecco perché l'accelerazione è negativa.
Ricaviamo t dalla prima equazione:
t = x / V0x
e sostituiamo nella seconda:

La gittata corrisponde al punto in cui y = 0:

La velocità del proiettile quando tocca terra è la risultante della velocità orizzontale che è rimasta sempre costante dall'inizio del moto e della velocità verticale data dalla relazione:
V(t) = Voy - g∙t
in cui:
V0y = 0
mentre il tempo t lo calcoliamo come il tempo necessario per il proiettile di percorrere la distanza di gittata con moto rettilineo uniforme alla velocità costante di 200 m/s:
t = 452/200 = 2,26 s
V(2,26) = - 9,8 ∙ 2,26 = - 22,14 m/s (il segno meno è dovuto al fatto che la velocità verticale è rivolta verso il basso)
Per cui la velocità del proiettile quando tocca suolo sarà:
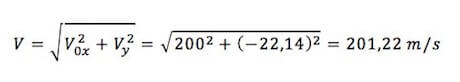
Studia con noi