Rendimento di un ciclo termico
Esercizio sul calcolo del rendimento di un ciclo termico
Una mole di gas ideale monoatomico subisce il ciclo descritto in figura:
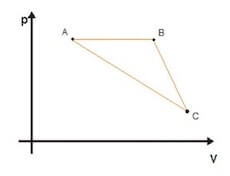
Sapendo che:
PA =1 bar
PC = 0,2 bar
VA = 10-2 m3
VB = 3 ∙ 10-2 m3
VC = 4 ∙ 10-2 m3
determinare il rendimento del ciclo.
Per un ciclo termico il rendimento η è il rapporto tra il lavoro prodotto dalla macchina termica e il calore assorbito:
η = L / Qa
Ora il lavoro totale prodotto durante il ciclo è l'area racchiusa dalla curva nel grafico, essendo questa figura un triangolo calcoliamo il lavoro come:
L = base ∙ altezza / 2
La base di questo triangolo è il lato AB mentre l'altezza relativa ad AB è PB – PC.
Il lato AB è la variazione di volume VB – VA.
AB = VB – VA = (3 – 1) ∙ 10-2 m3 = 2 ∙ 10-2 m3
Sapendo che la trasformazione AB è un'isobara (retta orizzontale) allora:
PB = PA = 1 bar = 105 Pa (per info: bar ia Pascal)
PC = 0,2 bar = 0,2 ∙ 105 Pa
Dunque:
h = PB – PC = (1 – 0,2) ∙ 105 Pa = 0,8 ∙ 105 Pa
Allora il lavoro totale compiuto durante il ciclo vale:
L = 2∙ 10-2 ∙ 0,8 ∙ 105 / 2 = 0,8 ∙ 103 J = 800 J
Dobbiamo adesso determinare per ogni singola trasformazione se si tratta di calore acquisito o ceduto attraverso il primo principio della termodinamica.
Per la trasformazione che è isobara (avviene cioè a pressione costante) il calore può essere calcolato come:
QAB = Cp ∙ n ∙ ∆T
in cui Cp è il calore specifico a pressione costante, n il numero di moli e ∆T la variazione di temperatura.
Calcoliamo le due temperature TA e TB attraverso l'equazione di stato dei gas perfetti:
TA = PA ∙ VA / (n∙R) = 105∙10-2 / (1 ∙ 8,314) = 120,3 K
TB = PB ∙ VB / (n∙R) = 105∙3∙10-2 / (1 ∙ 8,314) = 360,8 K
QAB = Cp∙n∙∆T = 5/2 ∙R ∙ 1 ∙ (360,8 – 120,3) = 5000 J (trattasi dunque di calore assorbito).
Determiniamo adesso la temperatura in C:
TC = PC ∙ VC /(n∙R) = 0,2∙105∙4∙10-2 / (1 ∙ 8,314) = 96,2 K
Relativamente alla trasformazione BC la variazione di energia interna ∆U è data da:
∆UBC = Cv∙n∙∆T = 3/2 ∙ 8,314 ∙ (96,2 – 360,8) = -3300 J
Il lavoro invece è l'area del trapezio rettangolo che ha come basi PB e PC e come altezza (VC – VB):
LBC = (1 + 0,2) ∙105 ∙ (4 – 3 ) ∙ 10-2 ∙ ½ = 600 J
Dunque dal primo principio della termodinamica determiniamo QBC:
QBC = ∆UBC + LBC = -3300 + 600 = -2700 J (trattasi dunque di calore ceduto).
Relativamente alla trasformazione CA la variazione di energia interna ∆U è data da:
∆UCA = Cv∙n∙∆T = 3/2 ∙ 8,314 ∙ (120,3 – 96,2) = 301 J
Il lavoro invece è l'area del trapezio rettangolo che ha come basi PA e PC e come altezza (VA – VC, trattandosi di compressione deve essere negativo):
LCA = (1 + 0,2) ∙105 ∙ (1 – 4 ) ∙ 10-2 ∙ ½ = -1800 J
Dunque dal primo principio della termodinamica determiniamo QCA:
QCA = ∆UCA + LCA = 301 - 1800 = -1500 J (trattasi dunque di calore ceduto).
Pertanto l'unico calore assorbito è QAB = 5000 J.
Allora il rendimento sarà:
η = L / Qa = 800 / 5000 = 0,16
che corrisponde a un redimento percentuale del 16%.
Studia con noi