Moto di un protone in un campo magnetico
Esercizio sul moto di un protone in un campo magnetico
Un protone si sta muovendo con velocità pari a 9,8 ∙ 107 m/s lungo la direzione dell'asse x quando incontra un campo magnetico uniforme di intensità 0,5 T uscente dal foglio e che si estende tra la coordinata x = 0 ed x = 1 m. Il campo magnetico fa curvare la traiettoria del protone.
Calcolare l'angolo che il protone forma con l'asse x all'uscita della regione di spazio sede del campo magnetico e le coordinate del punto di uscita. (Si sappia che la massa del protone è pari a 1,67∙10-27 kg).
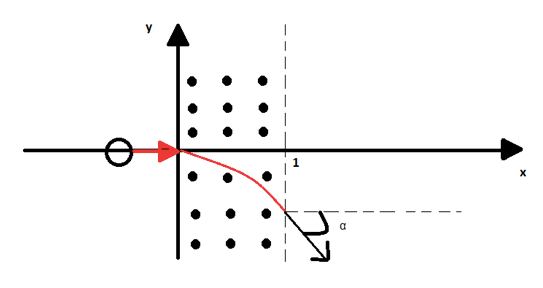
Svolgimento dell'esercizio
Il problema tratta il moto di una particella carica all'interno di un campo magnetico. Sappiamo che quando una carica q viene posta in una regione dello spazio ad una certa velocità v in cui è presente un campo magnetico di modulo B su di essa agirà una forza magnetica detta forza di Lorentz.
L'espressione della forza di Lorentz è un prodotto vettoriale tra due vettori, il vettore velocità e quello relativo al campo magnetico (in grassetto le grandezze vettoriali e con ⋀ si indica il simbolo del prodotto vettoriale):
F = q ∙ v ⋀ B
Ricordiamo che il modulo della forza espressa attraverso il prodotto vettoriale è il prodotto tra carica, modulo della velocità, modulo del campo magnetico ed il seno dell'angolo tra la velocità e il campo magnetico:
|F| = q ∙ v ∙ B ∙ senα
Nel nostro caso l'angolo tra la velocità del protone e le linee di campo magnetico vale 90° essendo i due vettori perpendicolari.
Visto che la velocità e il campo magnetico sono disposti tra di loro formanti un angolo di 90° in tal caso il seno dell'angolo vale 1 e il protone si muoverà di moto circolare uniforme; la forza magnetica si comporta come una forza centripeta che fa variare direzione e verso della velocità della carica istante per istante ma non ne fa variare il modulo (la forza magnetica non compie lavoro in quanto perpendicolare allo spostamento). Il raggio della traiettoria circolare vale:
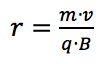
Possiamo allora costruire la seguente figura con angoli e triangoli rettangoli:
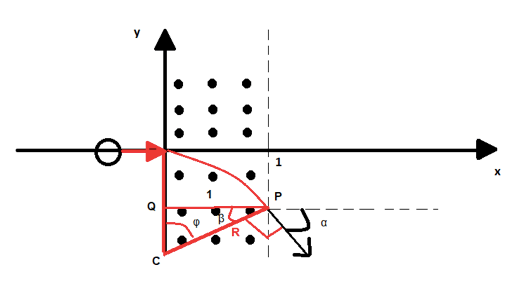
La particella sta descrivendo un arco di circonferenza di raggio R pari a:
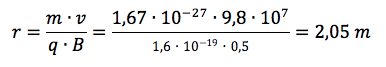
Nella nostra figura il raggio è stato indicato con il segmento CP. Dalla trigonometria sappiamo che:
CP ∙ senφ = QP
Ma QP non è altro che 1:
CP ∙ senφ = 1
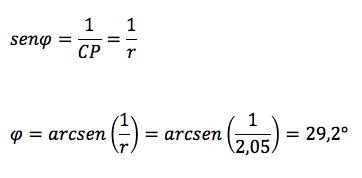
Poiché la somma degli angoli interni di un triangolo rettangolo vale 180°:
β = 180° - 90° - 29,2° = 60,8°
Adesso analizziamo l'angolo piatto in P. Esso è dato dalla somma di α, dell'angolo di 90° che il vettore velocità tangenziale forma col raggio e dall'angolo β:
180° = α + 90° + β
E dunque:
α = 180° - 90° - β = 29,2°
Per calcolare invece la coordinata y del punto P cioè la misura del segmento OQ consideriamo che OC = r e quindi:
OQ = r - QC
E QC è calcolabile a partire dalla trigonometria:
QC = r ∙ cosφ
Allora:
OQ = r – QC = r - r ∙ cosφ = r∙ ( 1 - cos φ) = 2,05∙ ( 1 -cos29,2)= 0,26 m
Link correlati:
Esercizio su un fascio di protoni che deve essere curvato di 90°
Quali sono le differenze tra il campo magnetico e il campo elettrico?
Calcolo della coefficiente di autoinduzione di un solenoide
Studia con noi