Esercizio su vettori piani
Esercizio svolto su vettori piani
Siano 
e 
due vettori piani, dimostrare che:
a) | - | ≥ || - ||
b) | + | ≤ || + ||
Svolgimento
I due vettori dati sono vettori piani, ovvero dotati di due componenti ciascuno x ed y:
= = (ax ; ay)
= (bx ; by)
Partiamo dalla prima relazione da dimostrare:
| - | ≥ || - ||
La relazione dice che il modulo della differenza dei due vettori è certamente maggiore o uguale alla differenza dei moduli dei due vettori presi singolarmente.
Proviamo a riscrivere a partire dalle componenti:
- = (ax - bx ; ay - by)
Per cui il modulo è
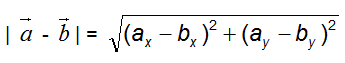
Scriviamo ora l'espressione per calcolare il modulo di ogni singolo vettore:
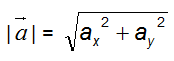
e
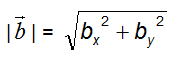
Quindi:
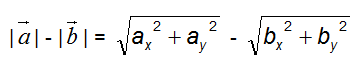
Ritornando alla disuguaglianza da verificare, poiché i moduli sono tutti termini positivi, possiamo elevare al quadrato ambo i membri:
| - |2 ≥ (|| - ||)2
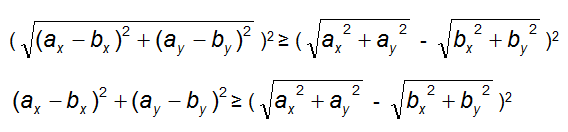
da cui svolgendo i calcoli:
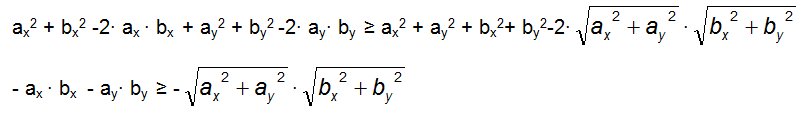
Cambiando di segno moltiplicando per -1 e ricordando di cambiare il verso della disuguaglianza a causa el prodotto per -1, otteniamo:
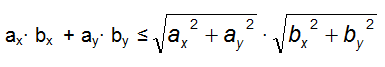
Eleviamo al quadrato ambo i membri:
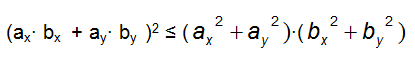
Ma l'espressione (ax · bx + ay · by) altro non è che il prodotto scalare a partire dalle componenti di e :
(ax · bx + ay · by) = x
Per cui:
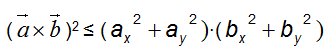
(ax2 + ay2) e (bx2 + by2) sono i moduli al quadrato dei rispettivi vettori:
( x )2 ≤ |a|2 · |b|2
Ricordando che dati due vettori e e detto θ l'angolo tra di essi, il prodotto scalare tra essi risulta pari a:
x = |a| · |b| · cosθ
Allora:
|a|2 · |b|2· cos2 θ ≤ |a|2 · |b|2
che risulta sempre verificata in quanto
cos2 θ ≤1
Dimostriamo adesso che
| + | ≤ || + ||
Analogamente al caso precedente:
Scriviamo ora l'espressione per calcolare il modulo di ogni singolo vettore:
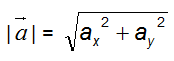
e
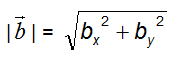
Quindi
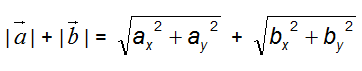
Ritornando alla disuguaglianza da verificare, poiché i moduli sono tutti termini positivi, possiamo elevare al quadrato ambo i membri:
| + |2 ≤ (|| + ||)2
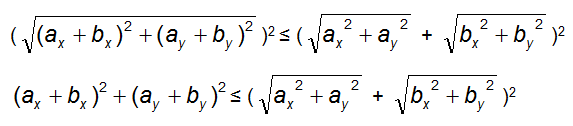
da cui svolgendo i calcoli:
che si riconduce al caso precedente già verificato.
Studia con noi