Esercizio su urto obliquo anelastico
Esercizio svolto su urto obliquo anelastico
Una sfera di massa m lanciata a velocità v ne urta una seconda inizialmente ferma e della stessa massa.
L'urto tra le due è obliquo e le due sfere procederanno dopo l'urto la prima in una direzione che forma un angolo di 45° con la direzione della velocità iniziale, mentre la seconda sotto alla direzione della prima formante un angolo di 30 ° con la direzione iniziale.
Calcolare le velocità delle due sfere dopo l'urto e la perdita di energia cinetica in valore numerico e percentuale.
Svolgimento dell'esercizio
La situazione descritta dal testo dell'esercizio può essere rappresentata nel seguente modo:
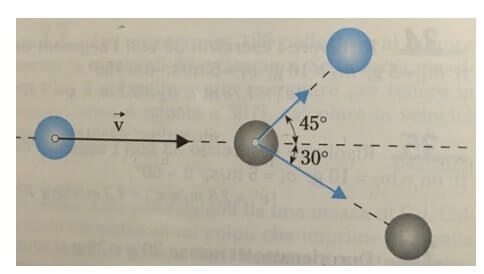
Si tratta di un urto obliquo anelastico con perdita di energia. Procediamo dunque ad imporre che la quantità di moto iniziale sia pari a quella finale tramite l'equazione vettoriale:
Qi = Qf
Scomponiamo il vettore quantità di moto e dunque anche il vettore velocità lungo le due direzioni x e y, scelto un comune sistema di assi cartesiani.
All'inizio la massa m possiede solo una componente orizzontale della velocità, in quanto il vettore velocità v risiede proprio sull'asse x. Per cui la quantità di moto su y è nulla.
Allora scriveremo che:
Qix = m∙v
Qiy = 0
Dopo l'urto invece le due velocità hanno direzioni tali per cui possiedono entrambe una componente x ed una componente y.
In particolare lungo la direzione orizzontale le due componenti saranno orientate verso il lato positivo dell'asse mentre sull'asse y la componente della prima sarà rivolta verso l'alto (positivo) e quella della seconda verso il basso (negativa).
Qfx = m∙V1∙cos45 +m∙V2∙cos30 = √2/2∙ m∙V1 + √3/2∙ m∙V2
Qfy = m∙V1∙sen45 -m∙V2∙sen30 = √2/2∙ m∙V1 - ½∙m∙V2
In cui V1 e V2 sono i moduli delle velocità finali da ricavare.
Imponiamo la conservazione della quantità di moto sia su x sia su y:
Qix = Qfx
m∙v= √2/2∙m∙V1 + √3/2∙m∙V2
Qiy = Qfy
0 = √2/2∙ m∙V1 - ½∙m∙V2
Poniamo a sistema le due precedenti:
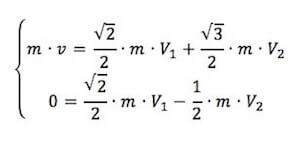
Semplifichiamo m visto che compare in tutti i termini, si ha che:
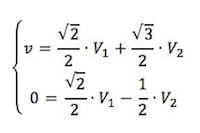
Sottraiamo membro a membro le due precedenti:
v – 0 = √2/2∙V1 + √3/2∙ V2 –(√2/2∙ V1 - ½∙V2)
v = √2/2∙ V1 + √3/2∙ V2 - √2/2∙ V1 + ½∙V2
v = √3/2∙ V2 + ½∙ V2
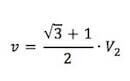
Da cui:
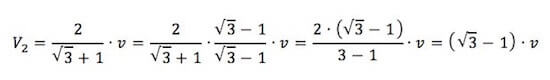
Ricaviamo ora V1 dalla seconda equazione:
0 = √2/2∙V1 - ½∙V2
Moltiplichiamo per 2
0 = √2 ∙V1 - V2
V1 = V2/√2
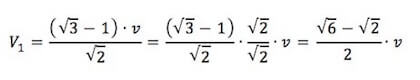
Quindi le due velocità valgono:
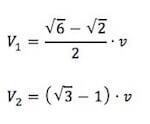
Per il calcolo della perdita di energia procediamo col quantificare l'energica cinetica sia nello stato iniziale sia in quello finale.
Ki = ½ ∙ m ∙ v2
Kf = ½ ∙ m ∙ V12 + ½ ∙ m ∙ V22
Kf = ½ ∙ m ∙ [ (6+2-2∙√12)/4 ∙v2 + (3 +1 -2∙√3)∙v2]
Kf = ½ ∙ m ∙ v2 ∙[ (8-2∙√12)/4+4-2∙√3]
Kf = ½ ∙ m ∙ v2 ∙ [ (8-4∙√3)/4 + 4 - 2∙√3]
Kf = ½ ∙ m ∙ v2 ∙[4∙(2-√3)/4 +4 - 2∙√3]
Kf = ½ ∙ m ∙ v2 ∙[2-√3+4 - 2∙√3]
Kf = ½ ∙ m ∙ v2 ∙[6 - 3∙√3]
Kf = 3/2 ∙ m ∙ v2 ∙[2 - √3]
La perdita di energia vale
Epersa = Kf - Ki = 3/2 ∙ m ∙ v2 ∙[2 - √3] - ½ ∙ m ∙ v2
Epersa = m ∙ v2 ∙ [3/2 ∙(2 - √3) - ½ ]
Epersa = (5-3∙√3)/2∙ m ∙ v2
In percentuale
Epersa/Ki = [(5-3∙√3)/2∙ m ∙ v2] / [ ½ ∙ m ∙ v2] = 5-3∙√3 = - 0,196 ovvero 19,6% (percentuale energia persa).
Studia con noi