Esercizio su urto completamente anelastico
Esercizio svolto su un urto completamente anelastico
Un proiettile di massa m viene lanciato con velocità V contro un pendolo di massa M legato ad un filo di lunghezza L e riemerge dall'altro lato con velocità V/2.
Calcolare quale deve essere la minima velocità V del proiettile affinché il pendolo esegua mezzo giro.
Svolgimento dell'esercizio
Trattandosi inizialmente di urto completamente anelastico imponiamo che la quantità di moto del sistema si mantenga la stessa prima e dopo l'urto (si veda: conservazione della quantità di moto).
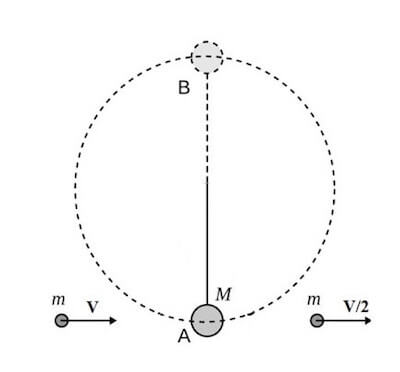
All'inizio l'unico corpo a possedere velocità è il proiettile m, mentre dopo l'urto sia il proiettile sia il blocco M avranno una loro velocità rispettivamente pari a V/2 e VA, per cui scriviamo che:
Qi = Qf
m ∙ V = M ∙ VA + m ∙ V/2
M ∙ VA = m ∙ V - m ∙ V/2
M ∙ VA = m ∙ V/2
Per cui la velocità cui la massa M del pendolo si inizia a muovere è pari a
VA = (m ∙ V) / (2 ∙ M)
Affinché il pendolo compia mezzo giro imponiamo che l'energia iniziale del sistema, che ha solo componente cinetica, sia pari all'energia posseduta alla fine del sistema, che scelto come sistema di riferimento 0 la posizione A sarà composta solo da energia potenziale gravitazionale a quota 2 volte la lunghezza del filo.
Per cui:
½ ∙ M ∙ VA2 = M ∙ g ∙ 2 ∙ L
Semplifichiamo M:
½ ∙ VA2 = g ∙ 2 ∙ L
VA2 = g ∙ 4 ∙ L
Da cui:
![]()
Ma ricordando la relazione trovata prima:
VA = (m ∙ V) / (2 ∙ M)
Si ha che:
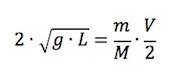
Per cui la velocità V del proiettile risulta:
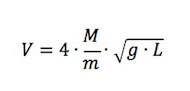
Studia con noi