Corpi che muovono di moto rettilineo uniforme partendo dalla stessa posizione con accelerazioni diverse
Esercizio su corpi che muovono di moto rettilineo uniforme partendo dalla stessa posizione con accelerazioni diverse
Due automobili partono dalla medesima posizione da ferme.
La prima accelera a 3 m/s2 per 10s, poi continua di moto rettilineo uniforme alla stessa velocità.
La seconda accelera a 2 m/s2 per 20s e poi mantiene la velocità.
Trovare il tempo e la distanza in cui i due veicoli si incontrano.
Svolgimento
Il problema presenta la situazione di due corpi che si stanno muovendo inizialmente di moto rettilineo uniforme partendo dalla stessa posizione con accelerazioni diverse.
In particolare le due accelerazioni con cui si muovono i due corpi sono:
a1 = 3 m/s2
a2 = 2 m/s2
Per cui le due leggi orarie relative ai due moti sono:
S1 = ½ · a1 · t2 = ½ · 3 · t2 = 3/2 · t2
S2 = ½ · a2 · t2 = ½ · 2 · t2 = t2
Dopo 10 s la prima auto raggiunge una velocità di
V1 = a1 · t = 3 · 10 = 30 m/s
e avrà percorso uno spazio di
So1 = 3/2 · t2 = 3/2 · 102 = 150 m
e mantiene costante la propria velocità mentre la seconda avrà percorso uno spazio di:
So2 = t2 = 102 = 100 m
La seconda sta ancora accelerando fino a t = 20 s quando avrà raggiunto una velocità di:
V2 = a2 · t = 2 · 20 = 40 m/s
Ed avrà percorso uno spazio di
S2 = t2 = 202 = 400 m
Infine dopo 20 s i due corpi si muoveranno entrambi di moto rettilineo uniforme.
Pertanto possiamo distinguere tre distinti intervalli di tempo:
- per t che va da 0 s a 10 s le due auto accelerano ognuna con la propria accelerazione;
- per t che va da 10 s a 20s la prima auto si muoverà a velocità costante mentre la seconda continuerà ad accelerare con la propria accelerazione;
- per t superiore a 20 s le due auto si muoveranno di moto rettilineo uniforme entrambe.
L'esercizio chiede il punto in cui la seconda auto sorpassa la prima.
La risoluzione prevede quindi la ricerca di tale punto ponendo a sistema via via per ogni intervallo di tempo la legge oraria che regola il moto dei due corpi.
Partiamo dal primo intervallo per t che va da 0 s a 10 s:
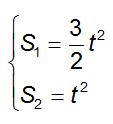
Poniamo S1 = S2 per verificare se ci sono punti di contatto in tale frangente di tempo:
S1 = S2
3/2 · t2 = t2
che non ha soluzioni. Questo vuol dire, come era intuibile, che nei primi 10 s non vi è alcun sorpasso.
Poniamoci adesso nel secondo intervallo per t che va da 10 s a 20s:
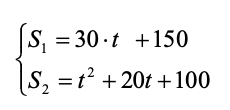
Le due leggi orarie rappresentano il moto dei due corpi: il primo si sta muovendo adesso di moto rettilineo uniforme con velocità costante (30 m/s) e si trova già per t = 10 s a 150 m dal punto di partenza.
Il secondo si sta ancora muovendo di moto rettilineo uniformemente accelerato avrà raggiunto una velocità di 20m/s (2∙10) e si trova per t = 10 s a 100 m dal punto di partenza.
Poniamo:
S1 = S2
30 · t + 150 = t2 + 20 · t + 100
t2 + 100 - 150 - 10 · t = 0
t2 - 10 · t - 50 = 0
che è una equazione di 2° grado.
Risolvendo l'equazione di secondo grado e scartando la soluzione negativa, priva di significato fisico, otteniamo:
t = 13,7 s
Il risultato non è accettabile: ci si è posti infatti nella condizione di mettere il punto dei 10 secondi come origine, quindi il tempo reale sarebbe 10 + 13,7 = 23,7 s, valore fuori dall'intervallo 10 - 20 s.
Consideriamo infine un terzo sistema per valutare se ci può essere un sorpasso nell'ultimo intervallo temporale, ovvero per t > 20 s.
In t = 20s il primo corpo avrà percorso i 150 m che aveva percorso durante i primi 10 s più lo spazio che percorrerà muovendosi a 30 m/s per altri 10 s:
S1 = 30 · t + 150 = 30 · 10 + 150 = 450 m
Il secondo invece
S2 = t2 = 202 = 400 m
Calcoliamo la velocità raggiunta dalla seconda auto in 20 s e con la quale procederà:
V = a2 · t = 2 · 20 = 40 m/s
Per cui il sistema sarà:
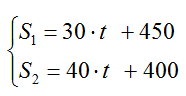
S1 = S2
30 · t + 450 = 40 · t + 400
40 · t - 30 · t = 450 - 400
10 · t = 50
t = 5 s
ovvero le due auto si incontrano 5 s dopo lo scatto che abbiamo considerato lo scatto dei 20 s, cioè a 25s.
In quei 5 secondi per cui lo spazio percorso sarà:
S = 30∙5 + 450 = 600 m dall'origine
(avremmo anche potuto calcolarla utilizzando S2 pervenendo allo stesso risultato)
Studia con noi