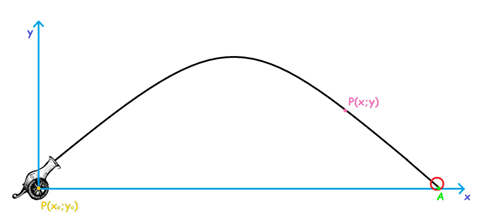
Moto parabolico con lancio obliquo
Esercizio sul moto parabolico con lancio obliquo
Un cannone spara un proiettile ad una velocità di 200 m/s che forma un angolo di 40° col suolo.
Trovare velocità e posizione del proiettile dopo 20 s.
Trovare inoltre dopo quanto tempo il proiettile atterrerà e a quale distanza dal punto di lancio.
Svolgimento
Si tratta di un moto parabolico con lancio obliquo, ovvero con velocità iniziale inclinata di un angolo α = 40° rispetto all'orizzontale e quindi composta da due componenti: quella orizzontale Vox e quella verticale Voy.
Cominciamo col calcolare posizione e velocità dopo 20 s:
Scriviamo le due leggi orarie che descrivono il moto nelle due direzioni x e y:
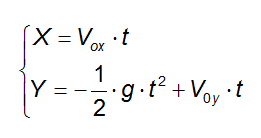
Sostituendo i dati:
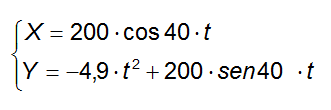
Pertanto quando t= 20 s la posizione x e y saranno rispettivamente:
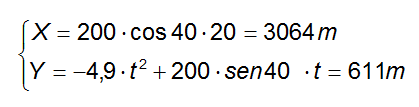
Per quanto riguarda invece la velocità dopo 20 s, essa avrà sempre due componenti x e y: la componente x sarà rimasta sempre la stessa dall'inizio in quanto il moto lungo l'orizzontale è di tipo rettilineo uniforme cioè a velocità costante, mentre la velocità lungo y sarà determinabile a partire dalla legge che lega velocità e tempo in un moto rettilineo uniformemente accelerato:
Vx(20) = V0x = 200 · cos40 = 153,2 m/s
Vy(20) = - g · t + Voy = -9,8 · 20 + 200 · sen40 = -67,4 m/s
Il fatto che la velocità lungo y sia negativa, vuol dire che tale componente è rivolta nel verso contrario rispetto a quello scelto come orientamento positivo, ovvero sarà rivolta verso il basso:
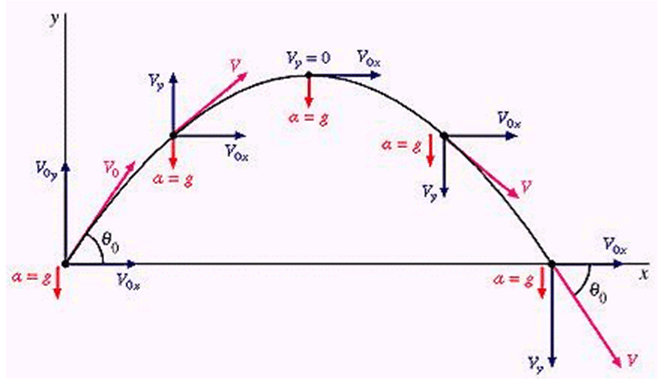
Come si evince dalla figura sopra, mentre la velocità orizzontale rimane costante, quella verticale inizialmente rivolta verso l'alto e quindi positiva, inizia a decrementare fino ad annullarsi (vertice della traiettoria).
Dopo di che sarà rivolta verso il basso fino a quando tocca il suolo e il suo valore sarà uguale ma opposto a quella iniziale.
Il modulo della velocità V dopo 20 s sarà:
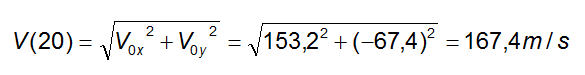
Calcoliamo infine la gittata, ovvero il cammino orizzontale percorso prima di toccare terra, che vale:
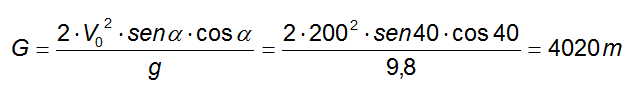
Il tempo impiegato a percorrere tale distanza è calcolabile attraverso la legge oraria su X:
t = G/Vox = 4020/153,2 = 26,24 s
In definitiva la posizione del proiettile dopo 20 s sarà nel punto di coordinate x = 3064 m e y = 611 m; la velocità dopo 20 s varrà 167,4 m/s.
La gittata del proiettile è 4020 m ed il tempo di atterraggio 26,24 s.
Link correlati:
Quali sono le formule sul moto parabolico?
Studia con noi