Gittata nel moto parabolico
Calcolo della gittata in un moto parabolico
Un aereo in volo che si sta muovendo lungo una traiettoria rettilinea orizzontale, parallela al suolo, con velocità di 200 m/s lascia cadere un pacco che tocca terra dopo 12 s.
Calcolare a che altezza si trova l'aeroplano, quanto vale la distanza orizzontale percorsa dal pacco e la velocità con cui tocca il suolo.
Svolgimento
La situazione descritta dal problema corrisponde a quella di un moto parabolico. Infatti l'oggetto lasciato cadere dall'aereo continuerà a muoversi di moto rettilineo uniforme lungo l'asse x e di moto rettilineo naturalmente accelerato lungo y, formando così un arco di parabola come traiettoria:
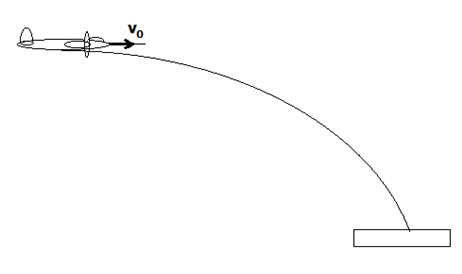
I dati forniti sono:
Vox = 200 m/s
∆t = 12 s
Scriviamo le equazioni che descrivono il moto del pacco durante la sua caduta:
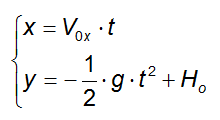
in cui Ho è l'altezza a cui viaggia l'aeroplano.
Sappiamo che il pacco tocca terra dopo 12 s, per cui y sarà uguale a 0 (quota del suolo) quanto t = 12 s:
0 = - 4,9 · 122 + H0
H0 = 705,6 m
La distanza orizzontale sarà pari al prodotto della velocità orizzontale per il tempo in cui rimane in volo, per cui si ha che:
X = 200 · 12 = 2400 m = 2,4 km = 2,4 km (chilometri)
Infine per trovare la velocità con cui tocca il suolo, dobbiamo considerare che nel punto in cui il pacco atterra, esso avrà due componenti di velocità: quella orizzontale che è rimasta costante durante tutto il moto ed una componente verticale calcolabile tramite la legge della velocità di un moto rettilineo uniformemente accelerato:
Vy(t) = g · t + Voy
Ora il pacco non aveva alcuna componente iniziale della velocità iniziale lungo y, per cui:
Voy = 0
e dopo 12 s:
Vy(12) = 9,8 · 12 = 117,6 m/s
La velocità risultante sarà per la regola del parallelogramma:
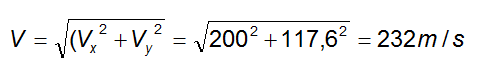
In definitiva l'altezza a cui si trova l'aereo vale 705,6 m; la distanza orizzontale percorsa dal pacco prima di toccare suolo è 2400 m e la velocità con cui esso atterra 232 m/s.
Link correlati:
Quali sono le formule sul moto parabolico?
Studia con noi