Moto armonico di un pendolo
Esercizio sul moto armonico di un pendolo
Un pendolo di lunghezza 1,2 m che oscilla muovendosi di moto armonico, è portato su un altro pianeta.
Quando viene messo in funzione si osserva che il pendolo compie 100 oscillazioni complete in 280 s.
Qual è dunque l'accelerazione di gravità su quel pianeta?
Svolgimento
Il problema riguarda la trattazione del moto oscillatorio relativo ad un pendolo.
Un pendolo è costituito da un corpo legato ad un estremo attraverso un filo inestensibile di lunghezza L; quando il corpo viene lasciato libero di muoversi il tipo di moto è oscillatorio e segue le leggi del moto armonico.
In particolare detta L la lunghezza del filo e g l'accelerazione di gravità, si ha che il periodo di oscillazione del pendolo vale:
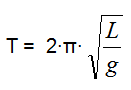
Dai dati a disposizione ricaviamo che:
L = 1,2 m
La frequenza f è data da:
f = 100/280 = 0,36 Hz
Ricordando che il periodo T è l'inverso della frequenza:
T = 1 / f = 1 / 0,36 = 2,8 s
Ricaviamo ora la formula inversa, partendo da quella del periodo, per ricavare l'accelerazione di gravità g.
Eleviamo ambo i membri al quadrato:
T2 = 4 · π2 · L / g
Da cui:
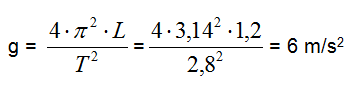
Dunque nel pianeta in questione, l'accelerazione di gravità ha un valore di 6 m/s2.
Link correlati:
Quali sono le formule del moto armonico?
Che cosa sono il periodo e la frequenza di un pendolo?
Studia con noi