Elettrone accelerato da un campo elettrico
Esercizio su elettrone che viene accelerato da un campo elettrico
Un elettrone viene accelerato attraverso un campo elettrico facendogli raggiungere una velocità di 1,6 ·106 m/s.
L'elettrone dunque percorre una zona di spazio in cui è presente un campo magnetico uniforme le cui linee di forza sono perpendicolari alla velocità della particella.
Calcolare il modulo del campo magnetico necessario affinché l'orbita circolare percorsa dall'elettrone abbia un raggio di 9,1 cm.
Svolgimento
La situazione fisica descritta dal problema è quella relativa ad un elettrone dotato di velocità v che si muove in un campo magnetico le cui linee di forza sono perpendicolari alla velocità:
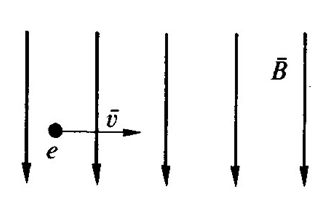
I dati a nostra disposizione sono:
m = 9,1 ·10-31 kg (massa dell'elettrone)
e = 1,6 ·10-19 C (carica dell'elettrone)
v = 1,6 ·106 m/s
R = 9,1 cm = 9,1 ·10-2 m
Sulla carica in moto nel campo magnetico agirà la forza di Lorentz, la cui direzione sarà perpendicolare alla velocità con cui l'elettrone penetra nel campo.
Dunque la traiettoria seguita dall'elettrone sarà di tipo circolare e la composizione dei due moti (moto circolare uniforme e moto rettilineo uniforme), darà luogo ad una traiettoria elicoidale:
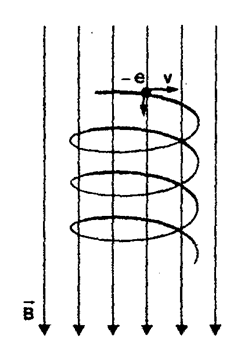
Ora la forza di Lorentz eguaglierà la forza centripeta che permette il moto circolare per cui:
Florentz = Fcentripeta
Da cui
q · V · B · senα = m · V2 / R
in cui
- q è la carica della particella
- V la sua velocità
- B l'intensità del campo magnetico
- α l'angolo tra V e B, essendo perpendicolari α = 90 e quindi sen90 = 1
- m la massa della particella
- R il raggio della traiettoria circolare.
Riordinando i termini e semplificando otteniamo che:
B = (m · V) / ( q · R) = (9,1 ·10-31 · 1,6 ·106) / (1,6 ·10-19 · 9,1 ·10-2) = 10-4 T
Per cui l'intensità del campo magnetico che permette di mantenere l'elettrone su un'orbita circolare di raggio 9,1 cm è pari a 10-4 T.
Link correlati:
Esiste il monopolo magnetico?
Calcolo del valore del campo magnetico al centro di due spire
Studia con noi