Moto elicoidale
Che cos'è il moto elicoidale?
Preso un sistema di riferimento cartesiano tridimensionale x,y,z consideriamo il moto di una particella che si muove a velocità v nel sistema di riferimento.
Se il moto della particella è di tipo circolare uniforme su un piano formato da due assi (cioè se agisce una forza centripeta su quel piano) e di tipo rettilineo uniforme lungo l'asse perpendicolare allo stesso piano allora la particella si muoverà di moto elicoidale.
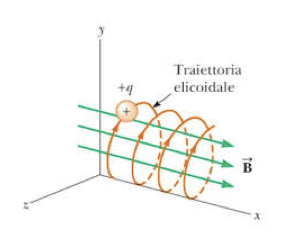
Il moto elicoidale uniforme è una particolare composizione di due moti:
- circolare uniforme a velocità angolare costante lungo il piano y,z
- rettilineo uniforme lungo l'asse x
La forza centripeta in questo caso agisce sul piano yz e dunque risulta perpendicolare alla direzione di avanzamento lungo l'asse x.
Moto di una carica all'interno di un campo magnetico
Sappiamo che quando una carica q si muove con velocità di modulo v all'interno di un campo magnetico di intensità B su di essa agisce una forza magnetica.
Questa forza magnetica, detta forza di Lorentz, è pari al prodotto vettoriale tra il vettore velocità moltiplicato per la carica q ed il vettore campo magnetico:
![]()
Il modulo della forza di Lorentz è dato dal prodotto tra carica, modulo della velocità e modulo del campo magnetico per il seno dell'angolo compreso tra velocità della carica e campo magnetico:
F = q ∙ v ∙ B ∙ senα
Per stabilire direzione e verso di F si utilizza la regola della mano destra in cui il pollice si orienta nella direzione e nel verso della velocità e l'indice col campo magnetico. Il medio che risulterà perpendicolare ad entrambe le altre due dita sarà la direzione ed il verso della forza magnetica.
Poiché la forza di Lorentz è data dal prodotto vettoriale tra il vettore velocità moltiplicato per la carica q ed il vettore campo magnetico ed essendo il risultato di un prodotto vettoriale ancora un vettore perpendicolare ad entrambi i vettori che si stanno moltiplicando, risulterà che il vettore forza di Lorentz è perpendicolare al vettore velocità e dunque anche al vettore spostamento.
Ricordando che il lavoro svolto da una forza altro non è che il prodotto scalare tra forza e spostamento e che risulta nullo se forza e spostamento sono perpendicolari tra di loro, allora si può concludere che la forza di Lorentz non compie alcun lavoro sulla particella carica in quanto essa è perpendicolare allo spostamento della stessa.
Questo si traduce nel fatto che l'energia cinetica della carica in moto non varierà bensì varierà soltanto la sua traiettoria. Il moto della particella infatti da rettilineo si trasformerà in moto circolare uniforme se velocità e campo magnetico sono tra di loro perpendicolari (nel caso α = 90°) oppure in moto elicoidale se l'angolo di penetrazione nel campo è diverso da 90°.
Consideriamo un sistema di riferimento x,y in cui è presente un campo magnetico B orizzontale ed uniforme lungo l'asse x:
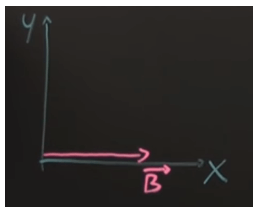
Ipotizziamo adesso che una carica entri con una velocità v inclinata di un certo angolo rispetto al piano x,y:
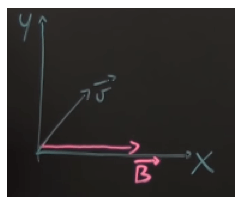
Se non ci fosse l'azione del campo la carica continuerebbe a muoversi imperturbata nel suo moto rettilineo. Il vettore v può essere scomposto infatti nelle due componenti vx e vy e la composizione del moto rettilineo uniforme lungo i due assi in assenza di campo magnetico B determina il moto rettilineo della carica nella sua direzione iniziale.
In presenza del campo magnetico invece i due moti rettilinei uniformi vengono modificati. In particolare lungo l'asse x agirà la forza di Lorentz di modulo pari a:
F = q ∙ vx ∙ B ∙ senα
in cui α è l'angolo tra la componente x della velocità e il campo magnetico. Essendo questo angolo uguale a 0 (i due vettori sono paralleli) anche il sen0 = 0 e allora non agirà alcuna forza lungo l'asse x.
Lungo l'asse y invece agirà la forza di Lorentz di modulo pari a:
F = q ∙ vy ∙ B ∙ senα
in cui α è l'angolo tra la componente y della velocità e il campo magnetico. Essendo questo angolo uguale a 90° (i due vettori sono perpendicolari) risulta che il sen90 = 1 e la forza:
F = q ∙ vy ∙ By
Questa forza per la regola della mano destra ponendo il polline nella direzione e verso di vy e l'indice nella direzione e verso di B è diretta entrante nel foglio:
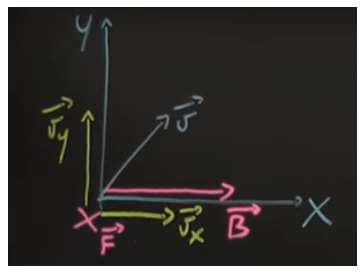
Il moto rettilineo uniforme lungo l'asse x dunque non viene perturbato mentre quello lungo l'asse y viene perturbato da una forza, quella di Lorentz appunto, e passa da moto rettilineo uniforme a moto circolare uniforme. La composizione sarà allora tra un moto circolare uniforme che avviene lungo un piano ortogonale al foglio ed un moto rettilineo uniforme su x.
Il moto risultante è un moto elicoidale uniforme che si propaga lungo x a passo costante, e la sezione dell'elica è una circonferenza con un certo raggio.
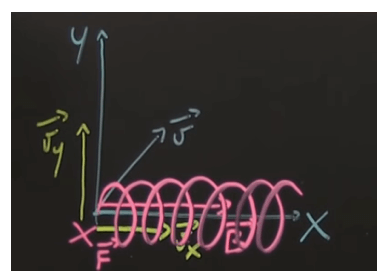
Angolo tra velocità e campo magnetico pari a 90°
Se la carica penetra all'interno del campo magnetico con la direzione della velocità perpendicolare alle linee di campo allora la particella inizierà a muoversi di moto circolare uniforme seguendo un'orbita circolare.
Si avrà uguaglianza tra la forza centripeta che agisce sulla particella in moto in traiettoria curvilinea e la forza di Lorentz per cui:
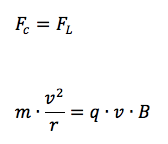
Da cui si può ricavare il raggio della traiettoria curvilinea pari a:
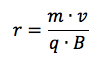
in cui m è la massa della particella, v il modulo della sua velocità, q la carica e B l'intensità del campo magnetico.
Angolo tra velocità e campo magnetico diverso da 90°
Se l'angolo α tra la direzione del vettore velocità della particella che entra nella regione di spazio sede del campo magnetico e le linee di campo è diverso da 90° (ed ovviamente da 0°) e quindi la velocità avrà anche una componente parallela al campo magnetico oltre che ortogonale, la particella proseguirà il suo moto con un moto elicoidale uniforme ovvero la composizione di un moto circolare uniforme lungo la direzione perpendicolare a B e di un moto rettilineo uniforme lungo la direzione di B. In questo caso si definiscono raggio e passo dell'elica le seguenti quantità:
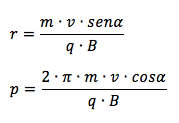
Link correlati:
Quali sono le formule del moto rettilineo uniforme?
Quali sono le formule inverse del moto rettilineo uniforme?
Studia con noi