Accelerazione lungo un piano inclinato
Calcolo della accelerazione lungo un piano inclinato
Calcolare l'accelerazione con cui scende un blocco di massa m lasciato libero di muoversi su di un piano inclinato di un angolo θ rispetto all'orizzontale.
Svolgimento esercizio
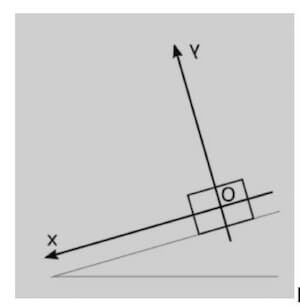
Per risolvere i problemi di statica e dinamica legati al piano inclinato, si ci riferisce sempre ad un sistema di assi cartesiani posizionati in maniera tale da risultare in linea col piano stesso.
L'asse delle x in particolare sarà scelto parallelo al piano così che l'asse delle y risulti ortogonale al piano di appoggio.
Sul corpo poggiato sul piano inclinato agiscono la forza normale di reazione del piano e la forza peso secondo il seguente diagramma di corpo libero:
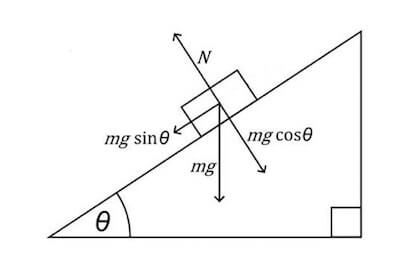
Poiché il corpo può muoversi unicamente lungo l'asse x applichiamo la seconda legge di Newton unicamente lungo quell'asse coordinato.
Avendo scelto come positivo il verso che è rivolto alla base del piano, sia m∙a sia m∙g∙sen θ sono positivi in quanto entrambi i vettori puntano verso il basso (il corpo sta scendendo).
Allora il risultato è che il corpo scenderà con accelerazione pari a:
m∙ g∙sen θ = m ∙a
da cui si deduce, risolvendo la precedente equazione, che il corpo scenderà con accelerazione:
a = g∙sen θ
È interessante notare il risultato in corrispondenza dei due angoli limite θ = 0° (piano orizzontale) e θ = 90° (piano perpendicolare al suolo).
Nel primo caso:
a = g ∙sen0 = 0
ovvero il corpo non accelera e quindi rimane fermo in assenza di altre forze agenti su di esso.
Nel secondo caso invece:
a = g ∙sen90 = g
ovvero il corpo scende in caduta libera (caduta dei gravi).
Studia con noi