Terza legge di Keplero
Enunciato della terza legge di Keplero
La terza legge di Keplero è stata scritta nel 1619 e quindi 10 anni dopo rispetto sia alla prima legge di Keplero che alla seconda legge di Keplero.
Spiegazione della terza legge di Keplero
La terza legge di Keplero afferma che: il rapporto tra il cubo del semiasse maggiore dell'orbita e il quadrato del periodo di rivoluzione è lo stesso per tutti i pianeti.
In formule, detto T il periodo di rivoluzione ed a il semiasse maggiore possiamo scrivere che:
T2 / a3 = costante
Ovviamente questa legge vale anche per il moto dei satelliti attorno ai pianeti.
Nel caso di approssimazione ad orbita circolare è possibile sostituire alla misura del semiasse la misura della distanza media di un pianeta dal Sole.
Dimostrazione della terza legge di Keplero
Supponiamo di considerare l'orbita di un pianeta di massa m2 intorno al Sole di massa m1 considerandola circolare.
Detta a la distanza media dall'astro e T il periodo di rivoluzione del pianeta, se la massa dell'astro è molto più grande rispetto a quella del pianeta, possiamo procedere ad uguagliare tra di loro la forza di attrazione gravitazionale e la forza centripeta che agisce sul pianeta:
Fgravitazionale = Fcentripeta
Ovvero:

Ma la velocità tangenziale v in un moto circolare uniforme, così come abbiamo approssimato il moto del pianeta, è pari alla circonferenza (orbita) diviso il periodo T, elevando poi tutto al quadrato.
Pertanto otteniamo:
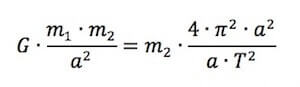
Riordinando i termini e operando le opportune semplificazioni otteniamo:
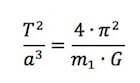
Per cui nel Sistema Solare nota la distanza dal Sole ed il periodo di un qualsiasi pianeta, si possono ricavare i periodi orbitali di tutti gli altri pianeti note le loro distanze dall'astro.
Esercizio #1
Sapendo che, nell'approssimazione di orbita circolare, la Terra ha un raggio orbitale pari a 1,50 ∙ 1011 m e che impiega 365,25 giorni a percorrerla interamente, determinare il raggio dell'orbita di Marte considerando che il suo periodo di rivoluzione è pari a 686,98 giorni terrestri.
Lo svolgimento dell'esercizio lo trovi qui: raggio dell'orbita di Marte.
Esercizio #2
Determinare la massa della Terra sapendo che la Luna impiega un periodo di 27,3 giorni terrestri a completare la sua orbita attorno alla Terra e che il raggio dell'orbita lunare è pari a 3,85 ∙ 105 km.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sulla terza legge di Keplero.
Studia con noi