Principio di Indeterminazione di Heisenberg
Principio di Indeterminazione di Heisenberg: definizione e spiegazione
Il fisico tedesco Heisenberg analizzando il modello atomico di Bohr, ne ravvisò i limiti, particolarmente per quanto riguarda le orbite che gli elettroni in esso compiono.
Parlare di orbite presuppone infatti di conoscere contemporaneamente la posizione e la velocità degli elettroni nei singoli istanti del loro moto.
Immaginiamo di volere determinare la posizione di un elettrone mediante irraggiamento con fotoni.
Affinché l'elettrone possa essere individuato, deve essere colpito da un fotone che venga deviato verso l'osservatore.
Il fotone, interagendo con l'elettrone, trasmette ad esso energia modificandone velocità e direzione.
Se, per evitare questo problema, scegliamo di usare un fotone a bassa energia, la lunghezza dell'onda a esso associata è così grande da rendere impossibile la determinazione della posizione.
Definizione del Principio di Indeterminazione di Heisenberg
In meccanica quantistica sono dette coniugate due grandezze il cui prodotto ha le dimensioni di un momento angolare.
Heisenberg riuscì a dimostrare che non è possibile conoscere contemporaneamente e con elevata precisione due variabili coniugate.
Si considerino le seguenti variabili coniugate:
- posizione x di una particella nella direzione x rispetto all'origine di un sistema di assi cartesiani
- quantità di moto p della medesima particella (si ricordi che p = m · v)
Le incertezze nella determinazione dei loro valori deve rispettare la seguente relazione:
![]()
in cui: ħ = h/(2π) è la costante di Planck ridotta (ħ si legga acca tagliato).
Questa relazione è nota come principio di indeterminazione.
In altre parole, se misuriamo contemporaneamente la posizione e la quantità di moto di una particella, nella determinazione dei loro valori, ogni grandezza sarà sempre determinata con una incertezza tale che il loro prodotto è sempre maggiore o uguale al valore ħ/2.
Si noti che l'incertezza sulla misura non deriva da una carenza delle tecniche di misurazione ma è una conseguenza della teoria della fisica quantistica.
Tale incertezza pone dei limiti a livello di precisione delle nostre misurazioni. Il miglior risultato ottenibile è quello per cui il prodotto delle indeterminazioni sulle due variabili coniugate è uguale a ħ/2, ovvero:
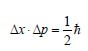
In questo caso le due indeterminazioni sono inversamente proporzionali.
Se Δx → 0, allora Δp → ∞.
Questo significa che se tentiamo di conoscere la posizione di una particella con una precisione assoluta allora l'incertezza sulla quantità di moto tende all'infinito e quindi non possiamo più avere alcuna informazione su questa grandezza.
Riferendosi ad un elettrone il principio può essere enunciato nel seguente modo: è impossibile conoscere nel medesimo istante e con la massima precisione la posizione e la quantità di moto di un elettrone.
Studia con noi