Grandezze derivate
Le grandezze derivate del Sistema Internazionale
Una grandezza fisica è una proprietà di un fenomeno, di un corpo o di una sostanza che può essere misurata.
Il Sistema Internazionale delle unità di misura classifica le grandezze fisiche in grandezze fondamentali e grandezze derivate.
Le grandezze derivate sono grandezze fisiche dipendenti; ciò significa che sono ricavabili dalle grandezze fondamentali mediante semplici operazioni aritmetiche (moltiplicazione, divisione).
Un esempio di grandezza derivata è la velocità.
Per determinare la velocità di un corpo non esiste una unità di misura specifica; tale grandezza è derivata in quanto dipende da altre due grandezze fondamentali che sono la lunghezza (misurata in metri) e il tempo (misurato in secondi).
Un altro esempio di grandezza derivata è il volume; esso viene misurato utilizzando come unità di misura il metro cubo (m3), ossia l'unità di misura della lunghezza elevata al cubo.
Esempi di grandezze derivate
Nella tabella seguente sono elencate alcune grandezze derivate; per ciascuna di esse è riportato il simbolo della grandezza, il nome dell'unità di misura e il simbolo dell'unità di misura.
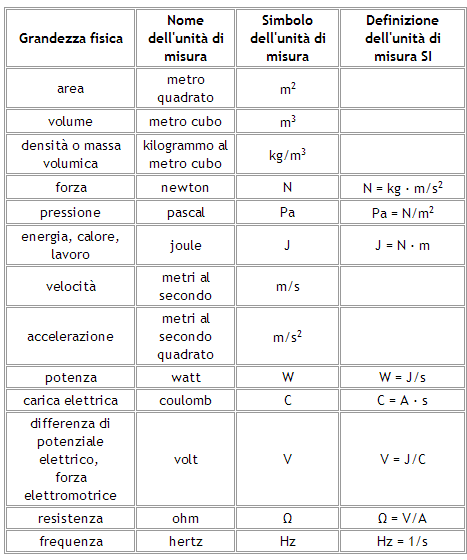
Per cercare di capire meglio il concetto di grandezze derivate, analizziamo nel dettagli alcune di queste e vedremo che le loro unità di misura derivano dalle unità di misura di due o più grandezze derivate combinate tra loro mediante semplici operazioni aritmetiche (moltiplicazione, divisione).
Ti potrebbe interessare: quiz sul Sistema Internazionale.
Così, ad esempio, sono grandezze derivate:
1) la forza, la cui unità di misura è il Newton. Il Newton è definito come la forza che imprime a un corpo di massa 1 kg l'accelerazione di 1 m/s2.
2) la pressione. L'unità di misura della pressione è il Pascal. Il Pascal è definito come la pressione esercitata dalla forza di 1 N applicata perpendicolarmente a una superficie di 1 m2 (metro quadrato).
3) la potenza, la cui unità di misura è il watt. Il watt è definito come la potenza di un sistema che produce il lavoro di 1 joule in un tempo di 1 s.
Link correlati:
Che cosa sono le misure dirette e indirette?
Studia con noi