Esercizio su un piano inclinato di 45°
Esercizio riguardante un piano inclinato di 45°
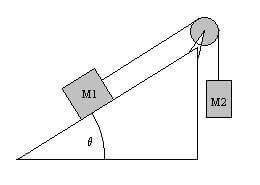
Su di un piano inclinato di un angolo di 45° rispetto all'orizzontale, è appoggiata una massa M1 = 50 kg.
Ad essa è collegata tramite una fune inestensibile e priva di massa ed attraverso una carrucola un'altra massa M2=16 kg, sospesa in aria.
Sapendo che il coefficiente di attrito relativo al piano vale μ = 0,25, stabilire se la massa M1 scende o sale lungo il piano e trovare l'accelerazione del sistema.
Svolgimento dell'esercizio
Il piano inclinato in questione ha un angolo rispetto all'orizzontale pari a α = 45° mentre le due masse valgono rispettivamente
M1 = 50 kg la massa poggiata sul piano
M2 = 16 kg la massa sospesa in aria,
Il piano è scabro e presenta coefficiente di attrito pari a μ = 0,25.
Per cui siamo in presenza della seguente situazione:
Il problema stabilisce di chiarire se la massa M1 sale o scende lungo il piano.
Ipotizziamo che la massa M1 possa salire lungo il piano e conseguentemente la massa M2 scendere verso il basso.
Rappresentiamo il diagramma di corpo libero per entrambe le masse.
Sulla massa M1 agiscono le seguenti forze:
- la forza peso
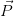diretta verticalmente verso il basso; - la tensione
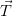della fune rivolta verso la carrucola; - la forza di reazione
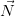perpendicolare al piano; - la risultante
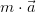diretta verso la carrucola del piano; - la forza di attrito
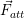che si oppone al moto e quindi poiché la massa sale, essa è rivolta verso la base del piano.
Sulla massa M2 invece:
- la forza peso 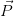diretta verticalmente verso il basso;
- la tensione 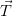della fune rivolta verso l'alto;
- la risultante 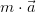diretta verso il basso, visto che per ipotesi la massa M1 sale e porta verso il basso la massa M2.
Possiamo dunque scrivere le equazioni scalari per M1 e M2.
Avremo per M1 lungo i due assi:
{T - Px - Fatt = M1·a
{N - Py = 0
Abbiamo scelto come positivo il verso con cui sta salendo la massa.
{T - M1·g·sen45 - μ·N = M1·a
{N = M1·g·cos45
Quindi:
{T - M1·g·sen45 - μ· M1·g·cos45 = M1·a
{N = M1·g·cos45
Per M2 avremo invece:
M2·g - T = M2·a
In questo caso abbiamo scelto come positivo il verso dell'asse rivolto verso il basso.
Prendiamo adesso in considerazione le due equazioni:
{T - M1·g·sen45 - μ· M1·g·cos45 = M1·a
{M2·g - T = M2·a
Ricaviamo T dalla seconda
T = M2·g - M2·a
e sostituiamo nella prima
T - M1·g·sen45 - μ· M1·g·cos45 = M1·a
M2·g - M2·a - M1·g·sen45 - μ· M1·g·cos45 = M1·a
Ricaviamo a:
M1·a + M2·a = M2·g- M1·g·sen45 - μ· M1·g·cos45
(M1 + M2) ·a = g· (M2 - M1· sen45 - μ · M1·cos45)
a = g· (M2 - M1·sen45 - μ· M1· cos45)/ (M1 + M2) = - 4,19 m/s2
tale risultato è però in disaccordo con le ipotesi iniziali in cui l'accelerazione era stata presa con verso positivo.
Per cui la massa M1 non può salire ma deve scendere.
Riscriviamo pertanto le equazioni considerando come positiva la discesa di M1 e la salita di M2:
{Px - T - Fatt = M1·a
{T - M2·g = M2·a
Dalla seconda
T = M2·g + M2·a
Sostituendo nella prima
M1·g·sen45 - (M2·g + M2·a) - μ· M1·g·cos45 = M1·a
M1·g·sen45 - M2·g - M2·a - μ· M1·g·cos45 = M1·a
(M1 + M2) ·a = g·( M1·sen45 - M2 - μ· M1·cos45)
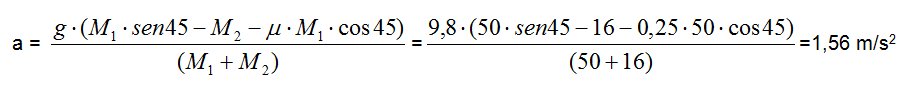
Per cui si può stabilire che la massa M1 scende verso il basso e l'accelerazione del sistema vale 1,56 m/s2.
Link correlati:
Quali sono le formule del piano inclinato?
Studia con noi