Esercizio riguardante l'inseguimento di auto
Esercizio di fisica riguardante l'inseguimento di auto
Un'automobile sta viaggiando alla velocità costante di 180 km/h quando sorpassa un'auto della polizia ferma che inizia un inseguimento verso l'auto.
L'auto della polizia accelera con un'accelerazione costante di 2 m/s2.
Quanta strada percorrerà l'auto prima di essere raggiunta dall'auto della polizia?
Svolgimento
Il problema presenta la situazione di un'auto che si sta muovendo di moto rettilineo uniforme che viene inseguita da un altro veicolo, quello della polizia, che si muove di moto rettilineo uniformemente accelerato.
Bisogna considerare i due moti contemporaneamente per poter determinare quale sarà il punto di contatto tra i due corpi cioè quando i due corpi occuperanno la stessa posizione.
Per far ciò scriviamo le due leggi orarie relative al moto dei due corpi e poniamole in un sistema affinché risolvendo il sistema ricaviamo l'eventuale punto di contatto tra le due curve che fisicamente si traduce nel ricavare il punto spaziale in cui i corpi si raggiungono ed occupano la stessa posizione.
Poniamoci pertanto nell'istante iniziale in cui l'auto sorpassa quella della polizia e quest'ultima inizia il suo moto e segniamo questo punto origine.
Per l'auto l'equazione oraria è:
S1 = V · t
La velocità dell'auto vale
V = 180 km/h = 180/3,6 m/s = 50 m/s
Quindi
S1 = 50 · t (legge oraria dell'auto)
Per quanto riguarda invece l'auto della Polizia, in questo caso si tratta di moto rettilineo uniforme accelerato con accelerazione costante pari a 2 m/s2, la cui legge oraria è:
S2 = ½ · a · t2 + Vo · t
L'auto parte da ferma, dunque
Vo = 0
In definitiva per l'auto della polizia:
S2 = ½ · 2 · t2 = t2 (legge oraria dell'auto della Polizia)
Il sistema sarà dato dunque da: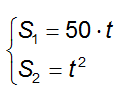
Poniamo che risulti:
S1 = S2
Ovvero che le due auto si raggiungano occupando la medesima posizione.
Pertanto possiamo procedere uguagliando membro a membro:
50 · t = t2
Riordinando i termini:
t2 - 50 · t = 0
raccogliamo t:
t · (t - 50) = 0
Le due soluzioni matematiche sono
t1 = 0 (soluzione corrispondente all'istante in cui le prima auto sorpassa la seconda auto ferma)
t2 = 50 s (soluzione corrispondente all'istante in cui l'auto della polizia raggiunge la prima auto)
In tale tale intervallo di tempo di 50 s le due auto avranno percorso uno spazio pari a:
S1 = S2 = 50 · t = 50 · 50 = 2500 m = 2,5 km
In definitiva l'auto prima di essere raggiunta dall'auto della polizia percorrerà 2,5 km.
Studia con noi