Compressione iniziale di una molla
Calcolo della compressione iniziale di una molla
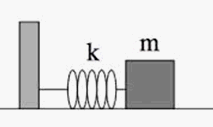
Un corpo di massa 1 kg, trattenuto da una molla orizzontale di costante elastica K = 400 N/m e compressa di una lunghezza pari a x, viene lasciato libero, acquisendo la velocità V, e procede lungo un piano scabro in cui il coefficiente di attrito dinamico vale 0,05.
Sapendo che il corpo arresta il proprio moto dopo aver percorso una distanza d = 21 m, calcolare la compressione iniziale della molla x.
Svolgimento
I dati forniti dal problema sono i seguenti:
m = 1 kg
K = 400 N/m
μ = 0,05
d = 21 m
Il problema può essere diviso in due parti distinte ma strettamente connesse tra di loro.
All'inizio, quando il tutto è nella fase statica, il corpo è trattenuto dalla molla che risulta compressa di una lunghezza pari a x, incognita del problema.
Pertanto la molla immagazzina una certa quantità di energia potenziale elastica data da:
Ep = ½ · K · x2
Successivamente quando il corpo viene rilasciato, questo procede di 21 m prima di fermarsi e quindi azzerare la sua velocità.
Quando la molla viene rilasciata e mette in moto il corpo, essa non fa altro che trasferire interamente la propria energia potenziale elastica al corpo sotto forma di energia cinetica.
Per cui la velocità iniziale con cui si muove la massa risulta di:
½ · K · x2 = ½ · m · V2
K · x2 = m · V2
Da cui:
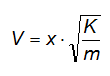
Una volta che il corpo si muove sul piano scabro con velocità iniziale pari a V e velocità finale pari a zero, perché arresta il suo moto, possiamo applicare il teorema dell'energia cinetica, detto anche teorema delle "forze vive", il quale afferma che il lavoro compiuto dalla risultante delle forze applicate su un corpo in un certo intervallo di tempo è uguale alla sua variazione di energia cinetica.
L = ΔEk
L'unica forza che compie lavoro in questa situazione è la forza di attrito, che risulta parallela allo spostamento.
Ricordiamo infatti che l'espressione con cui calcolare il lavoro è:
L = F · s · cosα
in cui
F è la forza
s lo spostamento
α l'angolo tra la forza e lo spostamento.
Poiché tale angolo è 0 nel caso dell'attrito, vuol dire che questa forza compie un lavoro non nullo.
Invece la forza di reazione N e la forza peso P, essendo perpendicolari allo spostamento (una è diretta verso l'alto, l'altra verso il basso) non compiono il lavoro in quanto in questo caso l'angolo è 90° e il cos90 = 0.
Ricordando che il modulo della forza di attrito vale:
Fattr = μ · m · g
Essendo questa diretta in direzione opposta al verso positivo dello spostamento, possiamo scrivere il lavoro compiuto dalla forza si attrito è:
L = - Fattr · d
Possiamo pertanto uguagliare questa ultima espressione alla variazione dell'energia cinetica:
L = ΔEk
- Fattr · d = ΔEk
- Fattr · d = ½ · m · Vi2 - ½ · m · Vf2
Ma poiché la velocità finale Vf è nulla:
- μ · m · g · d = - ½ · m · Vi2
Ricordando l'espressione che avevamo trovato precedentemente per la velocità iniziale in funzione delle caratteristiche della molla:
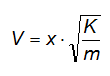
Sostituiamo ed otteniamo:
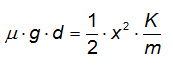
Da cui:
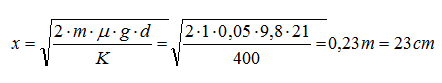
In definitiva la compressione iniziale della molla vale 23 cm.
Studia con noi