Tensione indotta in una bobina
Esercizio riguardante il calcolo della tensione indotta in una bobina
Una bobina è composta da 100 spire di area 100 cm2 e al suo interno viene fatto penetrare un campo magnetico ortogonale al piano della bobina con intensità variabile nel tempo partendo da intensità 0 ed arrivando a intensità pari a 0,8 T in un tempo pari a 10 s.
Sapendo che la bobina è collegata ad una resistenza da 5 Ω , calcolare la tensione indotta nella bobina e il lavoro totale speso nei 10 secondi.
Svolgimento
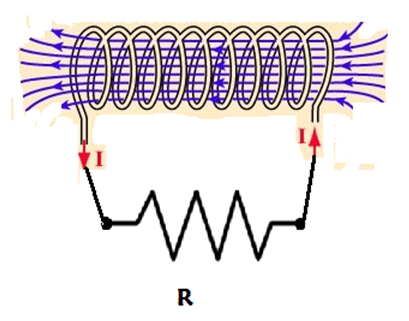
La bobina presentata dall'esercizio è sottoposta ad un campo magnetico variabile nel tempo.
Tale campo partendo da valore 0 raggiunge il valore di 0,8 T in 10 s.
Le linee del campo sono perpendicolari alla superficie della bobina, per cui la normale alla superficie e le linee di campo sono parallele (α=0).
I dati sono:
N = 100
S = 100 cm2 = 100 · 10-4 m2 = 10-2 m2
B1 = 0 T
B2 = 0,8 T
∆t = 5 s
R = 5 Ω
Se varia il campo magnetico all'interno della bobina, varierà anche il flusso del campo. Se vi è variazione di flusso nel tempo allora vi sarà una tensione indotta:
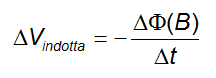
Che per N spire vale:
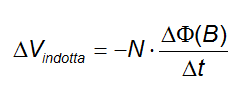
Ora ricordiamo che il flusso di un campo magnetico B attraverso una superficie piana S è il prodotto di S per la componente di B lungo la direzione perpendicolare a S:
Φ(B) = S · B · cosα
in cui
- S è la superficie di cui si deve calcolare il flusso del campo
- B è l'intensità del campo magnetico
- α è l'angolo che la direzione di B forma con la direzione perpendicolare alla superficie.
Per cui:
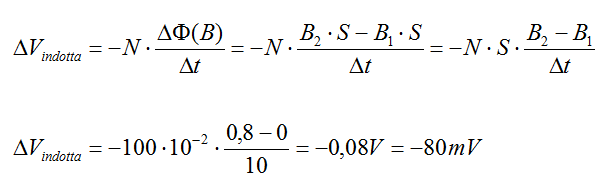
Il segno meno della tensione indotta deriva dalla legge di Lenz, in quanto la corrente che scaturisce dalla tensione indotta deve avere verso tale per cui il campo che essa genera si oppone al campo che viene fatto variare.
Ora il lavoro totale speso non è altro che il prodotto della potenza dissipata sulla resistenza per il tempo:
L = P · ∆t = ∆V · i · ∆t
Ma per la prima legge di Ohm:
i = ∆V / R
quindi
L = ∆V · i · ∆t = ∆V · (∆V / R) · ∆t = (∆V2 · ∆t ) / R
Sostituendo i dati in nostro possesso si ha che:
L = [(-0,08)2 · 10] / 5 = 0,0128 J = 1,28 · 10-2 J
Dunque la tensione indotta vale -80 mV (millivolt) mentre il lavoro vale 1,28 · 10-2 J.
Studia con noi