Protone accelerato ed immerso in un campo manetico
Esercizio su un protone accelerato ed immerso in un campo manetico
Un protone inizialmente fermo viene accelerato attraverso una ddp di 2500 V e viene immesso in una regione dello spazio in cui è presente un campo magnetico di intensità 0,3 T.
Determinare il raggio della traiettoria circolare che il protone percorre nel campo.
Svolgimento
I dati a nostra disposizione sono:
ΔV = 2500 V
mp = 1,67 ·10-27 kg (massa del protone)
q = 1,6 ·10-19 C (carica del protone)
B = 0,3 T
In seguito alla differenza di potenziale il protone acquisisce un'energia pari a:
E = q · ΔV = 1,6 ·10-19 · 2500 = 4 ·10-16 J
Tale energia ha solo componente cinetica, per cui la velocità con cui il protone penetra nel campo è pari a:
E = K = ½ · m · v2
da cui
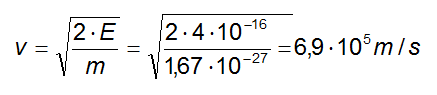
All'interno del campo magnetico, la forza di Lorentz che agisce sulla carica in movimento eguaglierà la forza centripeta che permette il moto circolare per cui:
Florentz = Fcentripeta
da cui
q · V · B · senα = m · V2 / R
in cui
- q è la carica della particella
- V la sua velocità
- B l'intensità del campo magnetico
- α l'angolo tra V e B e dato che l'angolo è 90, sen90=1
- m la massa della particella
- R il raggio della traiettoria circolare.
Ricaviamo dunque il raggio della traiettoria:
R = (m · V)/( q · B · sen α) = (1,67 ·10-27 · 6,9 · 105) / (1,6 ·10-19 · 0,3) = 24 · 10-3 m
Dunque il raggio della traiettoria descritta dal protone all'interno del campo magnetico è pari a 24 · 10-3 m.
Link correlati:
Che cos'è la forza magnetica?
Esercizio riguardante un filo conduttore percorso da corrente elettrica immerso in un campo magnetico
Studia con noi