Corpo lanciato radialmente alla superficie terrestre
Esercizio riguardante un corpo lanciato radialmente alla superficie terrestre
Un corpo viene lanciato radialmente alla superficie terrestre con velocità pari alla metà della velocità di fuga.
Determinare a quale distanza dal centro terrestre la velocità del corpo si annulla.
Svolgimento dell'esercizio
La velocità di fuga che un corpo deve possedere per sfuggire al campo gravitazionale terrestre, deriva dall'uguaglianza di energia cinetica ed energia potenziale gravitazionale e porta alla formula:
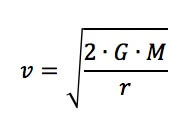
Ora se il corpo possiede una velocità pari a v/2 allora l'energia cinetica non sarà sufficiente a coprire tutta l'energia potenziale gravitazionale.
Pertanto il corpo arriverà ad una distanza h dal centro della Terra tale per cui possiederà un'energia potenziale gravitazionale pari alla somma dell'energia cinetica iniziale e dell'energia potenziale gravitazionale iniziale (ovvero quando si trova a distanza R dal centro della Terra):
½ ∙ m ∙ v'2 - Uo = - U
Ricordando di utilizzare i segni meno davanti all'espressione del potenziale!
Ricordando che:
U0 = G ∙ M ∙ m / R
e che:
U = G ∙ M ∙ m / h
Si ha che:

Semplifichiamo il segno meno, G, m ed M si ha che:
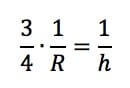
da cui otteniamo:
h = 4/3 ∙ R
Studia con noi