Sfera in rotazione lungo una circonferenza verticale
Esercizio svolto su una sfera posta in rotazione lungo una circonferenza verticale
Una sfera di massa m è posta in rotazione lungo una circonferenza verticale da una corda di lunghezza L.
La velocità della sfera vale Vb nel punto più basso della traiettoria mentre vale Va in quello più in alto.
Svolgimento dell'esercizio
L'esercizio propone il caso di una sfera di massa m posta in rotazione lungo una circonferenza verticale.
Sapendo che Vb è la velocità della sfera nel punto più basso e Va è la velocità della sfera nel punto più alto, si vuole determinare la tensione della corda nei due punti.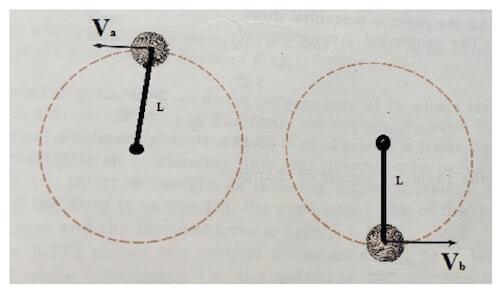
Consideriamo un sistema di assi cartesiani in cui studiare le forze in gioco nel problema:
Il problema distingue due ben precisi momenti: nel primo la sfera si trova nella posizione più in alto della traiettoria.
In questa posizione su di essa agisce la forza peso diretta verso il basso così come la tensione della fune.
La loro risultante è pari alla forza centripeta diretta verso il centro.
La seconda posizione è quella invece del punto più in basso in cui la forza peso è diretta verso il basso ma stavolta la tensione è rivolta come la forza centripeta, verso l'alto in direzione del centro.
I diagrammi di corpo libero sono:
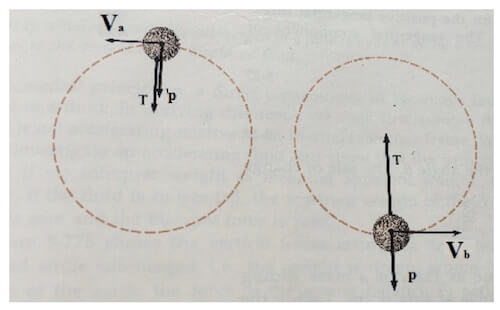
Consideriamo il primo momento.
Scriviamo la seconda legge di Newton riferendoci unicamente all'asse y:
-T - m∙g = -m∙Va2/L
Ogni termine ha il segno meno davanti perché abbiamo scelto come sistema di riferimento cartesiano una coppia di assi in cui l'asse verticale y è rivolto verso l'alto, mentre i tre vettori sono tutti rivolti verso il basso (direzione negativa).
Consideriamo il secondo momento.
T - m∙g = m∙Vb2 / L
Dunque possiamo ricavare il valore della tensione nei due casi risolvendo semplicemente le due equazioni:
T = m∙Va2/L - m∙g = m∙( Va2/L - g)
e
T = m∙g + m∙Vb2/L = m∙(g + Vb2/L)
Nel secondo caso, punto più basso, la tensione è dunque pari alla somma della forza peso più la forza centripeta.
Se la pallina infatti fosse ferma (V=0) non vi sarebbe più la componente centripeta e la tensione sarebbe solo pari alla forza peso (caso statico).
Nel punto più in alto invece la tensione è data dalla componente centripeta meno la forza peso.
Per cui per essere positiva la tensione e mantenere la corda tesa il termine della forza centripeta deve essere maggiore della forza peso:
m∙Va2/L > m∙g
ovvero:
Va >√(r∙g)
Se la velocità di rotazione della sfera è inferiore allora la tensione della corda viene meno e la palla abbandonerà la sua traiettoria circolare iniziandosi a muovere lungo una traiettoria parabolica (moto parabolico).
Studia con noi