Lavoro delle forze non conservative
Calcolo del lavoro delle forze non conservative
In un parco giochi, un uomo di 80 kg si lancia su di un tappeto elastico dall'altezza di 10 m.
Una volta atterrato sopra di esso, il tappeto si deforma abbassandosi di 1,75 m.
Determinare il valore della costante elastica nell'ipotesi che non intervengano forze dissipative.
Considerando che poi l'uomo viene fatto rimbalzare fino all'altezza di 3 m rispetto al livello del tappeto a riposo, determinare il lavoro delle forze non conservative che intervengono.
Svolgimento dell'esercizio
All'inizio l'uomo possiede esclusivamente energia potenziale gravitazionale, dovuta al fatto che si trova ad una certa altezza h.
Preso come riferimento zero, la quota a cui il tappeto si abbassa, ovvero 1,75m, l'altezza complessiva a cui si trova l'uomo utile ai fini del calcolo dell'energia potenziale gravitazionale vale:
h = 10 + 1,75 = 11,75 m
Una volta fermo, l'uomo possiederà invece energia potenziale elastica dovuta alla deformazione del tappeto elastico assimilabile come molla.
Per cui:
m ∙ g ∙ h = ½ ∙ K ∙ x2
Da cui:
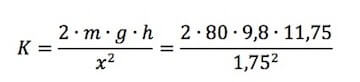
Quindi:
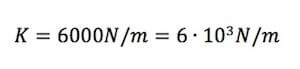
Pertanto, nel caso in cui non intervengano forze dissipative il valore della costante elastica è pari a 6 ∙ 103 N/m.
Quando l'uomo riparte verso l'alto consideriamo che all'inizio possiede esclusivamente energia potenziale elastica, mentre al termine della sua corsa, cioè quando arriva all'altezza h' di 3+1,75 = 4,75 m, possiederà solo componente potenziale gravitazionale dell'energia meccanica.
Nel frattempo però parte dell'energia meccanica si sarà degradata a causa della presenza delle forze dissipative; e tale quota di energia dissipata, pari al lavoro compiuto dalle forze non conservative, vale:
Lnc = U – Uel = m ∙ g ∙ h' – ½ ∙ K ∙ x2
Sostituendo i dati in nostro possesso si ha che:
Lnc = 80 ∙ 9,8 ∙ 4,75 – 0,5 ∙ 6000 ∙ 1,752 = -5463 J
Ovvero:
Lnc = -5,5 ∙ 103 J
Pertanto il lavoro delle forze non conservative è pari a -5,5 ∙ 103 J.
Studia con noi