Esercizio sulla regola del parallelogramma
Esercizio svolto e commentato sulla regola del parallelogramma
Una barca sta attraversando perpendicolarmente alle sponde un fiume, la cui corrente ha velocità di 5 m/s.
Se la barca ha una velocità di 15 m/s calcolare il modulo del vettore velocità risultante, la sua direzione ed il suo verso rispetto alle rive.
Svolgimento
Nella situazione descritta dal problema sono presenti due vettori relativi alla velocità della barca e a quella dell'acqua del fiume.
Di tali vettori conosciamo:
- il modulo:
Vb = 15 m/s velocità della barca
Va = 5 m/s velocità dell'acqua - la direzione:
essi sono perpendicolari tra di loro ovvero formano un angolo di 90° - il verso:
la barca va da est verso ovest, l'acqua da nord verso sud (convenzioni arbitrarie del nostro sistema di riferimento)
In definitiva possiamo rappresentare tale situazione con il seguente disegno:
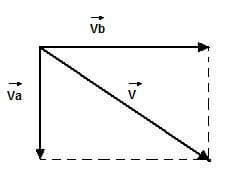
Ora la velocità risultante 
è la somma vettoriale delle due componenti 
e 
:
Dal punto di vista grafico la risultante è pertanto quella indicata in figura, disegnata sfruttando la regola del parallelogramma, che consiste nel rappresentare i vettori a due a due con la stessa origine ed individuare la loro risultante somma come la diagonale del parallelogramma avente per lati i due vettori stessi.
Per quanto riguarda invece il modulo di utilizziamo il teorema di Pitagora:
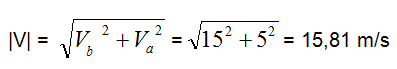
Ovviamente il verso sarà quello che va dalla riva di partenza a quella di origine; mentre per calcolare l'angolo che la risultante forma con , quindi con la corrente dell'acqua, possiamo utilizzare considerazioni trigonometriche.
Detto α tale angolo sappiamo che:
V·sen α = Vb
V·cos α = Va
Dividendo membro a membro le due suddette uguaglianze otteniamo:
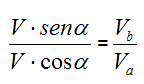
Da cui:
ed infine:
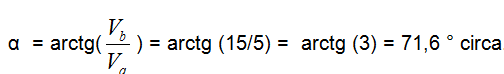
Per cui la velocità con cui si muoverà la barca sarà pari a 15,81 m/s in modulo ed inclinata di 71,6° rispetto alla velocità della corrente.
Studia con noi