Esercizio che comprende il moto dei gravi e il moto rettilineo uniforme
Esercizio svolto che comprende il moto dei gravi e il moto rettilineo uniforme
Si lascia cadere un sasso in un pozzo vuoto.
Dal momento in cui si è lasciato libero il sasso trascorrono 6,8 secondi quando si ode il suono dell'urto del sasso con il fondo.
Sapendo che la velocità del suono nell'aria è di 330 m/s calcolare la profondità del pozzo.
Svolgimento
Chiamiamo h la profondità del pozzo.
Tale distanza è percorsa una volta in un tempo t1 dal sasso in caduta libera soggetto ad accelerazione di gravità g, lasciato libero di cadere a velocità iniziale nulla.
Dopo che il sasso ha raggiunto il fondo, parte il suono derivante dall'urto che percorre in un tempo t2 sempre la stessa distanza h.
Il tempo totale tra quando si lascia il sasso e quando si ode il suono è pari a:
T = t1 + t2 = 6,8 s
La prima parte del moto è di tipo rettilineo uniformemente accelerato, per cui lo spazio percorso vale:
h = ½ · g · t12
Una volta urtato il fondo, il suono procederà di moto rettilineo uniforme e si propagherà lungo la distanza h fino all'uscita del pozzo a velocità V = 330 m/s:
h = 330 · t2
Per cui abbiamo due stesse espressioni per ricavare h, che possiamo pertanto uguagliare tra di loro:
½ · g · t12 = 330 · t2
Sapendo che:
t1 + t2 = 6,8
scriviamo
t2 = 6,8 - t1
Per cui:
½ · g · t12 = 330 · (6,8 - t1)
Svolgiamo i calcoli
½ · 9,8 · t12 = 2244 - 330· t1
4,9 · t12 + 330· t1 - 2244 = 0
che rappresenta un'equazione di secondo grado in t1 da svolgere:
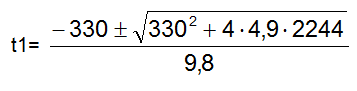
Delle due soluzioni scartiamo quella negativa ed otteniamo:
t1 = 6,22 s
e ricordando che
h = ½ · g · t12
otteniamo allora
h = 4,9 · 6,222 = 189,9 m
Per cui il pozzo è profondo circa 190 m ovvero 1,9 · 102 m.
Studia con noi