Esercizio sulla legge gravitazionale di Newton
Esercizio svolto sulla legge gravitazionale di Newton
Calcolare a quale altezza bisogna portarsi rispetto alla superficie della Terra affinché si dimezzi il proprio peso.
(raggio della Terra 6371 chilometri, massa della Terra 5,972 · 1024 kg)
Svolgimento
La forza peso a cui è soggetta qualsiasi massa presente sulla superficie terrestre, deriva direttamente dall'espressione della legge gravitazionale di Newton:
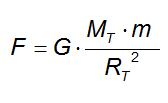
in cui MT e RT sono rispettivamente la massa e il raggio della Terra.
Riscrivendo la precedente come:
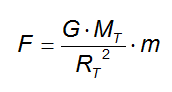
e sostituendo otteniamo:
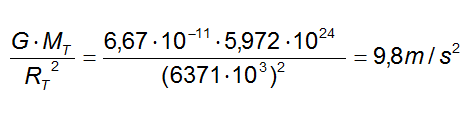
Abbiamo dunque ricavato il noto valore dell'accelerazione di gravità g che moltiplicato alla massa di un corpo posto sulla superficie della Terra ci restituisce il peso.
Ora, il problema ci chiede di calcolare a che altezza h portare un corpo di massa m affinché il peso di quest'ultimo dimezzi.
Detto P il peso originario sulla superficie della Terra pari a:
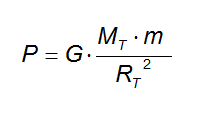
il peso P' quando la distanza dal centro del pianeta diventa (RT + h) sarà dunque:
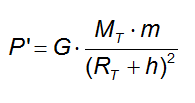
e sappiamo che
P' = ½ · P
Allora possiamo scrivere che:
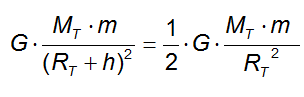
Semplifichiamo i termini G, MT e m in quanto presenti in ambo i membri:
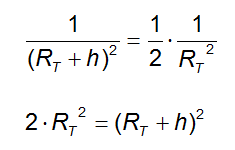
Sviluppiamo il quadrato di binomio:
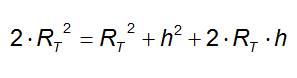
Riordiniamo i termini e portiamo in un solo membro:
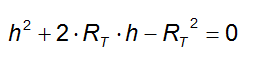
che rappresenta un'equazione di secondo grado in h.
Risolviamola:
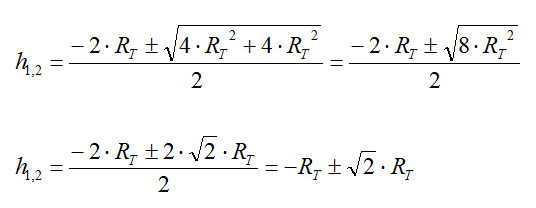
Scartiamo la soluzione negativa, per cui l'altezza desiderata risulta pari a:
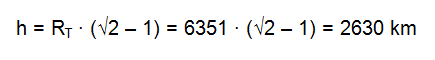
In definitiva il peso si dimezza ad una distanza di 2630 km dalla superficie terrestre.
Studia con noi