Calcolo della compressione di una molla
Esercizio sul calcolo della compressione di una molla
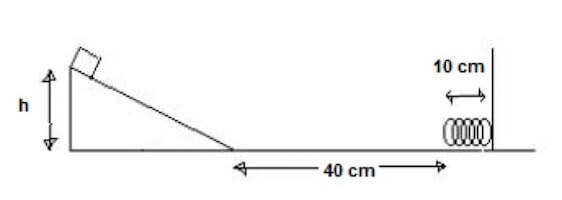
Un punto materiale di massa 20 g si trova ad una certa altezza h sopra un piano inclinato liscio.
Una volta lasciato libero, il punto percorre interamente il piano inclinato e procede lungo un piano orizzontale scabro caratterizzato da un coefficiente di attrito pari a 0,1.
Dopo aver percorso 40 cm incontra una molla con costante elastica pari a 2 N/m che si trova ad una lunghezza a riposo di 10 cm.
Determinare quale deve essere l'altezza iniziale h a cui deve essere posto il punto affinché esso nella sua discesa riesca a comprimere interamente la molla e toccare la parete a cui essa è agganciata.
Svolgimento dell'esercizio
Il problema va risolto con considerazioni prettamente energetiche.
Inizialmente il corpo possiede energia potenziale gravitazionale in quanto si trova ad una certa altezza h rispetto al livello del suolo.
Tale energia verrà in parte dissipata dall'attrito presente sul piano orizzontale e la restante parte si trasformerà in energia potenziale elastica dovuta alla compressione della molla.
In sostanza il bilancio energetico sarà di questo tipo:
Lnc = Uel – U
in cui:
- Uel è l'energia finale del sistema concentrata nella contrazione della molla mentre;
- U è l'energia iniziale.
Per cui possiamo scrivere che:
- μ ∙ m ∙ g ∙ d = ½ ∙ K ∙ x2 - m ∙ g ∙ h
Attenzione al segno del lavoro delle forze dissipative!
Sappiamo infatti che il lavoro di una forza di attrito è sempre negativo.
Il nostro obiettivo è ricavare h.
Dunque:
m ∙ g ∙ h = ½ ∙ K ∙ x2 + μ ∙ m ∙ g ∙ d
Da cui:
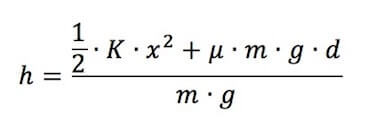
Sostituendo i dati in nostro possesso si ha che:

Pertanto, l'altezza iniziale h a cui il punto materiale deve essere posto affinché esso, nella sua discesa, riesca a comprimere interamente la molla e toccare la parete a cui essa è agganciata è di 9,1 cm.
Link correlati:
Quali sono le formule inverse dell'energia potenziale elastica?
Studia con noi