Bilancia di Cavendish
Esercizio sulla bilancia di Cavendish
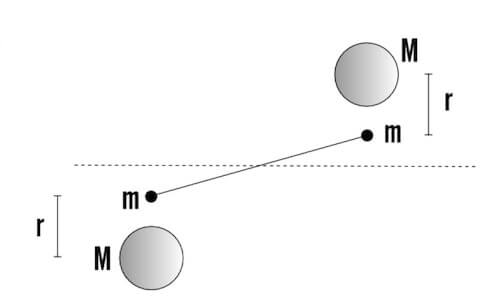
In una bilancia di Cavendish le masse delle sfere sono rispettivamente di 10 kg e 10 g (M e m della figura seguente).
Le due masse sono poste a 5 cm di distanza e l'asta su cui sono poste le due masse più piccole è lunga 20 cm.
Qual è la forza di attrazione tra la sfera grande e quella piccola?
Quale momento deve esercitare la sospensione attraverso il filo per bilanciare queste forze?
Svolgimento dell'esercizio
L'esercizio riguarda l'esperimento di Cavendish.
Elenchiamo dapprima i dati forniti dal problema:
- m1 = 10 kg
- m2 = 10 ∙ 10-3 kg
- r = 5 ∙ 10-2 m
- d = 20 ∙ 10-2 m
La forza di attrazione gravitazionale che si instaura tra le due masse e che quindi agisce sull'asta su cui sono sospese le piccole masse, facendone variare la rotazione, è pari a:
Fg = G ∙ (m1 ∙ m2)/ r2
Sostituendo i dati in nostro possesso si ha che:
Fg = 6,67 ∙ 10-11 ∙ (10 ∙ 10 ∙ 10-3) / (5 ∙ 10-2)2
da cui:
Fg = 26,7 ∙ 10-10 N
Il momento sarà pari al prodotto della forza di attrazione appena ricavata per il braccio d dell'asta:
M = Fg ∙ d
Da cui:
M = 26,7 ∙ 10-10 ∙ 20 ∙ 10-2 = 534 ∙ 10-14 N∙m
Studia con noi