Calcolo del prodotto scalare
Esempio di calcolo del prodotto scalare
Dati i vettori 
e 
di componenti rispettivamente:
= (1; -½; 1)
= (0, 0, 1)
si calcolino le componenti del vettore 
tale per cui risulti:
x = 0
x = 0
x = 1
Si calcoli inoltre il modulo del vettore .
Svolgimento
Sono dati i due vettori e di cui conosciamo le tre componenti spaziali; ci poniamo quindi in un sistema di riferimento a tre dimensioni.
Le componenti di e sono rispettivamente:
ax = 1
ay = -½
az = 1
bx = 0
by = 0
bz = 1
Sfruttiamo adesso le tre condizioni proposte dal testo per ricavare tante equazioni quante sono le incognite da trovare.
La richiesta del problema è quella di calcolare il vettore tale per cui risultino verificate contemporaneamente le seguenti richieste:
x = 0
x = 0
x = 1
Quindi poiché le incognite da trovare sono le componenti del vettore , che sono tre, lo stesso numero di equazioni è quello richiesto per procedere al calcolo.
Partiamo dalla prima condizione:
x = 0
Il prodotto scalare tra e deve essere nullo.
Ricordiamo che il prodotto scalare di due vettori a partire dalle loro componenti vale:
x = ax · cx + ay · cy+ az · cz = 0
Sostituendo otteniamo:
1· cx + (-½) · cy + 1·cz = 0
cx -½ · cy + cz = 0
La seconda condizione invece è:
x = 0
x = cx · bx + cy · by + cz · bz= cx · 0 + cy · 0+ cz · 1 = 0
cz = 0
Infine la terza ed ultima condizione:
x = 1
x = = cx · cx + cy · cy + cz · cz = 1
cx2 + cy2 + cz2 = 1
Ricapitolando le tre equazioni ricavate sono:
cx - ½ · cy + cz = 0
cz = 0
cx2 + cy2 + cz2 = 1
che rappresenta un sistema di tre equazioni in tre incognite.
Dalla seconda equazione abbiamo che
cz = 0
per cui sostituiamo nella prima:
cx - ½ · cy + cz = 0
cx - ½ · cy + 0 = 0
cx - ½ · cy = 0
cx = ½ · cy
Ora sostituiamo tutto nell'ultima equazione:
cx2 + cy2 + cz2 = 1
(½ · cy)2 + cy2 + 02 = 1
¼ · cy2 + cy2 + 02 = 1
¼ · cy2 + cy2 = 1
5/4 · cy2 = 1
cy2 = ⅘
Da cui:
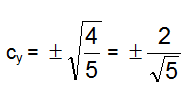
Poiché risultava:
cx = ½ · cy
allora avremo:
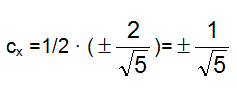
In definitiva allora avremo due vettori che soddisfano le condizioni iniziali:
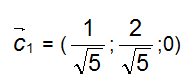
e
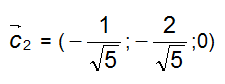
Il modulo dei due vettori appena ricavati coincide e vale:
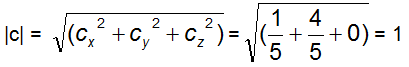
Studia con noi