Urto anelastico
Urto anelastico e completamente anelastico
L'urto rappresenta la collisione tra due o più corpi nello spazio e rappresenta un'interazione in cui si sviluppano forze di tipo impulsivo, ovvero forze che hanno intensità molto elevate ma che durano un brevissimo istante.
Poiché le forze esterne risultano trascurabili rispetto a quelle interne il sistema può benissimo essere considerato come isolato per cui nei fenomeni di urto la quantità di moto totale del sistema prima e dopo la collisione si conserva (si veda: conservazione della quantità di moto).
Un urto può essere di due tipi: urto elastico e urto anelastico. In questa sezione tratteremo la seconda tipologia di urto.
Urto completamente anelastico
Si definiscono anelastici quegli urti in cui non si conserva l'energia cinetica ma unicamente la quantità di moto, in particolare si parla di urti completamente anelastici quando dopo l'urto i due corpi rimangono attaccati l'un con l'altro procedendo insieme.
L'energia persa nell'urto si trasforma in altre forme di energia, ad esempio energia meccanica che serve alla deformazione dei corpi per poter procedere uniti.
È il tipico caso di tamponamento tra due auto nel quale parte dell'energia cinetica si trasforma in energia meccanica (deformazione della carrozzeria), energia acustica e calore.
Altro esempio si ha nel caso del pendolo balistico in cui un proiettile viene sparato contro un blocco e questo si porta ad una certa altezza col proiettile conficcato al suo interno.
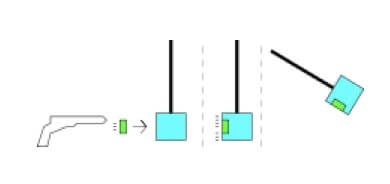
Pendolo balistico
Risoluzione di un problema di urto anelastico
Per la risoluzione di un problema in cui è presente un urto di tipo completamente anelastico si parte dall'impostare che la quantità di moto iniziale del sistema sia uguale alla quantità di moto finale.
Ricordiamo che la quantità di moto del sistema è la somma dei prodotti di ogni massa per la rispettiva velocità.
Nel caso di due corpi avremo:
Qi = m1 ∙ V1 + m2 ∙ V2
Dopo l'urto però i corpi formeranno un corpo unico di massa:
M = m1 + m2
Per cui la quantità di moto finale sarà pari a:
Qf = (m1 + m2) ∙ V
in cui V1 e V2 sono le velocità dei singoli corpi all'inizio, prima dell'urto, mentre V è la velocità con cui si muovono i corpi una volta che si sono urtati e sono rimasti incastrati.
Imponendo che:
Qi = Qf
Otteniamo:
m1 ∙ V1 + m2 ∙ V2 = (m1 + m2) ∙ V
da cui possiamo ricavare la velocità assunta dai due corpi dopo l'urto come:
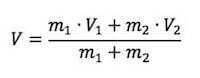
Poiché come già detto in un urto completamente anelastico l'energia cinetica non si conserva, in molti problemi è richiesto di determinare la perdita di energia del sistema.
Per calcolare tale variazione basta calcolare l'energia cinetica del sistema iniziale, data dalla somma dell'energia cinetica di ciascun corpo:
Ki = ½ ∙ (m1 ∙ V12 + m2 ∙ V22)
e l'energia cinetica finale:
Kf = ½ ∙ (m1 + m2) ∙ V2
La variazione rappresenta l'energia persa durante l'urto:
Epersa = ΔK = Kf - Ki
Esercizio
Un vagone ferroviario di massa 8000 kg che si sta muovendo alla velocità di 20 m/s urta un secondo vagone fermo identico al primo.
I due vagoni dopo l'urto procedono unitamente.
Determinare la velocità del sistema dopo lo scontro e la perdita di energia.
Lo svolgimento dell'esercizio lo trovi qui: perdita di energia in un urto completamente anelastico.
Esercizio
Un proiettile di massa m viene lanciato con velocità V contro un pendolo di massa M legato ad un filo di lunghezza L e riemerge dall'altro lato con velocità V/2.
Calcolare quale deve essere la minima velocità V del proiettile affinché il pendolo esegua mezzo giro.
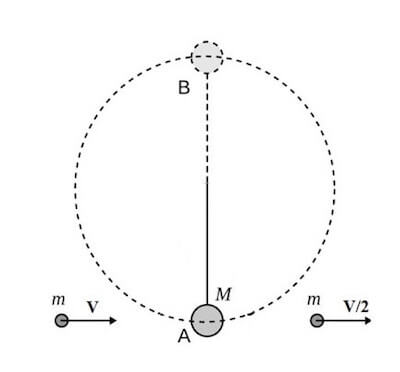
Lo svolgimento dell'esercizio lo trovi qui: esercizio su urto completamente anelastico.
Studia con noi