Piano inclinato
Piano inclinato ed equilibrio su un piano inclinato
In fisica per piano inclinato si intende una superficie piana inclinata rispetto al suolo e formante con esso un angolo α.
Il piano inclinato consente dunque a un corpo di elevarsi rispetto al suolo fino ad un'altezza h detta altezza del piano inclinato o viceversa di portarsi dall'altezza h al suolo, percorrendo una traiettoria non verticale. In altre parole il piano inclinato permette ad un corpo di giungere al suolo a partire da una certa quota h evitando la caduta libera o di raggiungere tale quota in maniera più agevole, evitando la salita verticale.
Dunque il piano inclinato rappresenta una macchina vantaggiosa di tipo semplice così come la leva.
La distanza orizzontale tra il punto di contatto al suolo e la proiezione al suolo del punto di massima elevazione del piano inclinato è detta distanza orizzontale indicata con d, mentre la distanza obliqua tra i due punti è detta lunghezza del piano inclinato L.

Rappresentazione di un piano inclinato.
Relazioni trigonometriche che interessano il piano inclinato
Da un punto di vista geometrico il piano inclinato è un triangolo rettangolo i cui cateti sono rappresentati dall'altezza h del piano e dalla distanza orizzontale d dello stesso.
La lunghezza del piano inclinato rappresenta l'ipotenusa del triangolo rettangolo.
È possibile applicare le relazioni trigonometriche per ricavare i vari elementi del piano inclinato:
- senα = h/L
- L ∙ senα = h
- L ∙ cosα = d
- tgα = h/d
Scelta del sistema di riferimento
Per risolvere i problemi di statica e dinamica legati al piano inclinato, si ci riferisce sempre ad un sistema di assi cartesiani posizionati in maniera tale da risultare in linea col piano stesso.
Il sistema di assi cartesiani rappresenta il nostro sistema di riferimento. L'asse delle x in particolare sarà scelto parallelo al piano così che l'asse delle y risulti ortogonale al piano di appoggio.
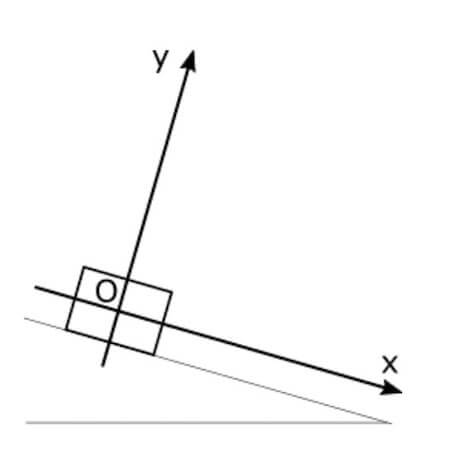
Sistema di assi cartesiani in un piano inclinato.
Forza peso in un piano inclinato
La forza peso è una forza sempre presente in quanto dipendente dalla presenza di una massa poggiata sul piano.
Essa è diretta verso il basso, lungo la verticale ortogonale al suolo, ed ha modulo pari al prodotto della massa per l'accelerazione di gravità:
|P| = m ∙ g
Per poter lavorare nel sistema di riferimento scelto, ovvero con l'asse x parallelo al piano inclinato, risulta necessario scomporre il vettore forza peso nella sua componente x ed y.
In particolare chiameremo componente perpendicolare della forza peso P⊥ e componente parallela della forza peso P// rispettivamente la componente y ed x:
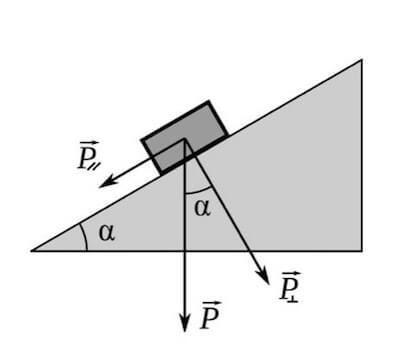
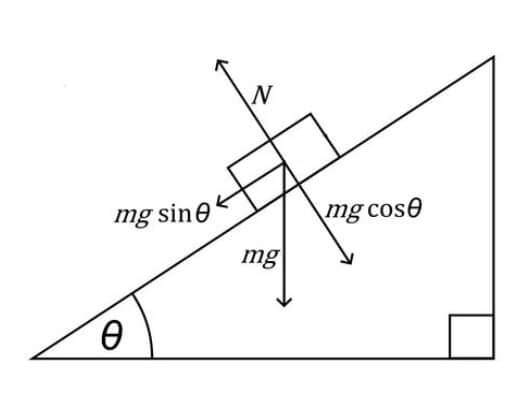
Osservando la figura precedente, per costruzione geometrica si deduce che lo stesso angolo α che esiste tra il piano inclinato ed il suolo, si viene a creare tra il vettore forza peso e l'asse y.
Per cui grazie alle proprietà trigonometriche dei triangoli possiamo scrivere che:
P⊥ = m ∙ g ∙ cosα
P// = m ∙ g ∙ senα
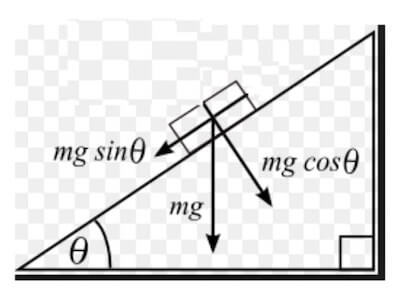
Forza normale nel piano inclinato
Un'altra forza sempre presente quando il corpo è poggiato sul piano è la forza normale N o reazione del piano.
È un vettore perpendicolare al piano di appoggio e rivolto verso l'alto.
Per cui questo vettore possiede solo componente verticale y nel sistema di riferimento scelto.
Nella figura seguente la forza normale è stata indicata con la lettera N.
La componente lungo l'asse x della forza normale è pari a zero.
Forza di attrito nel piano inclinato
Possono esistere due tipologie di piano inclinato: quello liscio e quello scabro.
Un piano inclinato è liscio quando la forza di attrito non è presente.
Il piano inclinato sarà invece detto scabro se è presente la forza di attrito FA .
La forza di attrito è un vettore che giace lungo l'asse x ed ha verso opposto a quello del moto.
Quindi se il corpo sta scendendo lungo il piano, sarà rivolta verso la sommità del piano inclinato, mentre se il corpo sta salendo la forza di attrito sarà rivolta verso la base del piano.
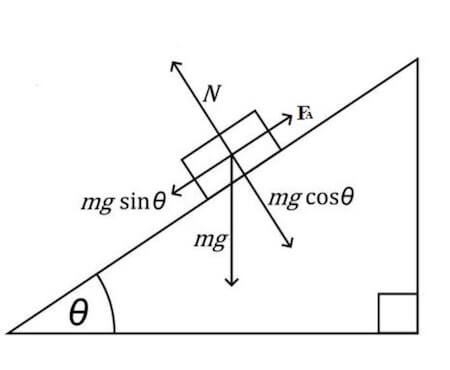
Ricordando che il modulo della forza di attrito è pari al prodotto del coefficiente di attrito per la normale:
FA = μ ∙ N
e che sull'asse y del piano inclinato la somma di tutte le forze deve essere zero, in quanto il corpo si sta muovendo unicamente lungo l'asse orizzontale, si ha che:
N – m ∙ g ∙ cosα = 0
per cui:
N = m ∙ g ∙ cosα
e la forza di attrito:
FA = μ ∙ N = μ ∙ m ∙ g ∙ cosα
Equilibrio su un piano inclinato
Immaginiamo di avere un piano inclinato liscio su cui è poggiato ad una certa altezza un corpo di massa m.
Allora le uniche forze agenti sul corpo sono la forza peso (componente parallela ed ortogonale) e la forza normale.
Lungo l'asse x, la seconda equazione della dinamica risulterà:
m ∙ g ∙ senα = m ∙ a
Avendo scelto come positivo il verso che è rivolto alla base del piano, sia
m ∙ a
che
m ∙ g ∙ senα
sono positivi in quanto entrambi i vettori puntano verso il basso (il corpo sta scendendo).
Allora il risultato è che il corpo scenderà di moto rettilineo uniformemente accelerato con accelerazione pari a:
a = g ∙ senα
e poiché l'angolo che può assumere un piano inclinato varia da 0 a 90° non compresi (0 < α < 90) il seno dell'angolo potrà variare tra 0 e 1 non compresi (0 < senα < 1), dunque l'accelerazione con cui scende il corpo in queste condizioni sarà sempre inferiore all'accelerazione di gravità g.
Affinché il corpo non scenda e rimanga in equilibrio sul piano è necessario che debba intervenire un'altra forza che bilanci la componente parallela della forza peso.
Questa altra forza potrebbe essere una forza di attrito (nel caso di piano scabro) o una qualsiasi forza esterna.
Esercizio
Un corpo di massa m = 30 kg è in equilibrio su di un piano inclinato liscio che forma un angolo di 30° con il suolo.
Il blocco è tenuto fermo tramite una fune inestensibile e priva di massa alla parete.
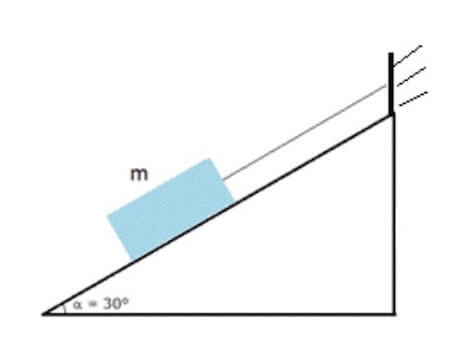
Calcolare la tensione della fune e il modulo della normale che agisce sul blocco.
Calcolare l'accelerazione con cui il corpo scende se la corda viene tagliata.
Lo svolgimento dell'esercizio lo trovi qui: equilibrio su un piano inclinato.
Esercizi sul piano inclinato
Li trovi qui: esercizi sul piano inclinato.
Link correlati:
Quali sono le formule del piano inclinato?
Che cos'è un argano?
Studia con noi