Onda armonica
Che cosa è un'onda armonica?
Le onde possono essere classificate in base alla natura della perturbazione che si propaga in onde elastiche ed elettromagnetiche:
- le onde elastiche sono tutti quei fenomeni ondulatori che riguardano perturbazioni che si propagano in corpi elastici e materiali, come ad esempio il suono o le onde lungo una corda tesa;
- le onde elettromagnetiche invece non necessariamente devono propagarsi attraverso un mezzo materiale, ma possono viaggiare anche nel vuoto; è il caso della luce.
Entrambe i tipi di onde possono essere "armoniche".
Ma cosa significa onda armonica? Quando un'onda è armonica?
Un'onda è detta armonica quando la sua legge di vibrazione è di tipo sinusoidale.
Pertanto, un'onda armonica è un'onda che propagandosi in un mezzo determina una variazione per ogni punto dello spazio rispetto al proprio stato di equilibrio in maniera periodica, ovvero con variazioni che si ripetono ad ogni intervallo di tempo detto periodo, e la cui legge di vibrazione risulta di tipo sinusoidale cioè descritta dalle funzioni seno o coseno.
Sono onde armoniche quindi le onde elastiche che si propagano lunga una corda tesa e determinano uno spostamento per ogni punto della corda, o quelle che si propagano lungo una sbarra metallica, oppure le onde sonore, le onde elettromagnetiche come le onde radio o la luce.
Ciò che differenzia tutte queste onde è la grandezza che oscilla: nel caso delle onde elastiche è la posizione, nel caso delle onde sonore è la pressione del mezzo, nel caso delle onde elettromagnetiche il valore di campo elettrico e del campo magnetico.
La legge delle onde armoniche in un punto fissato
Se immagiamo un'onda che si propaga lungo una corda e fissiamo l'attenzione su di un punto specifico P, vedremo che tale punto andrà su e giù rispetto alla propria posizione di equilibrio allo scorrere del tempo:
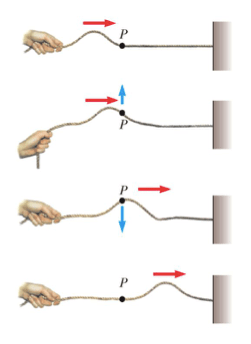
Se vogliamo riportare la posizione del punto P rispetto al tempo in un grafico otterremo come risultato:
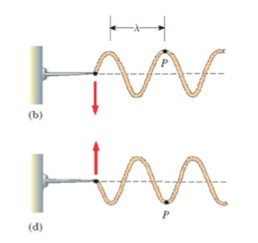
L'onda è tipo periodico ed il punto P oscilla verticalmente nella direzione y di moto armonico.
La legge di un'onda armonica che descrive questo movimento è del tipo :
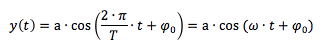
in cui:
- a: ampiezza dell'onda, rappresenta il valore del massimo (o del minimo) della curva;
- T: è il periodo dell'onda misurato in secondi;
- φ0 : rappresenta la fase iniziale dell'onda, ovvero se il suo grafico parte dall'origine che abbiamo fissato negli assi o risulta traslato, molto spesso è uguale a 0 e quindi non compare nell'espressione della funzione;
- ω: è la pulsazione dell'onda ed è pari al rapporto tra il doppio del π ed il periodo.
La legge di un'onda armonica ha grafico y-t del tipo:
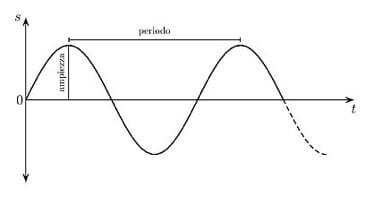
Nella rappresentazione dell'onda attraverso la sua equazione avremmo potuto utilizzare la funzione seno anziché la funzione coseno.
Ma sapendo che le due curve risultano identiche ma solo sfasate di π/2 tra di loro, concludiamo che l'equazione di un'onda è di tipo sinusoidale.
La legge delle armoniche per un istante fissato
Possiamo anche immaginare di voler disegnare il grafico dell'onda che ci permette di individuare quale sarà lo spostamento di ogni punto della corda in un dato istante di tempo.
In questo caso l'equazione sarà in funzione della posizione x lungo la corda:
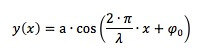
In questo caso λ rappresenta la lunghezza d'onda.
La legge generale delle onde armoniche
Abbiamo visto che per le onde elastiche è possibile esprimere la funzione che restituisce lo spostamento di ogni punto P lungo la corda sia in funzione del tempo t sia in funzione dello spazio x.
È possibile ricavare un'unica legge per le onde armoniche per cui y risulta essere funzione contemporaneamente di t e x:
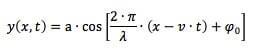
in cui v è la velocità in cui si muove l'onda. Abbiamo ricavato la funzione d'onda direttamente dalla formula:
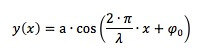
a cui abbiamo sostituito a posto dell'unica variabile posizione x la quantità x-v∙t che rappresenta il fatto che il profilo dell'onda in movimento alla velocità v corrisponde allo stesso profilo che un osservatore vedrebbe se si spostasse con velocità uguale ma opposta all'onda quindi -v e se l'onda fosse ferma.
Esercizio #1
Un'onda elastica è descritta dall'equazione:
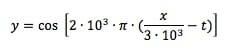
Determinarne l'ampiezza e la lunghezza d'onda.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sull'equazione di un'onda elastica.
Esercizio #2
L'equazione di un'onda armonica che si propaga lungo una corda è:
y = 0,02 ∙ cos[π ∙ (2∙x - 10∙t)]
Determinare frequenza, ampiezza, lunghezza d'onda e velocità.
Lo svolgimento dell'esercizio lo trovi qui: studio dell'equazione di un'onda armonica.
Studia con noi