Leva di secondo genere
Che cosa si intende per leva di secondo genere?
Una generica leva è una macchina semplice costituita da un'asta rigida su cui agiscono due forze, dette rispettivamente resistenza e potenza o forza motrice, ed indicate con R e P.
L'asta può ruotare attorno ad un punto fisso che viene detto fulcro della leva.
A seconda della posizione del fulcro rispetto a quella della resistenza e della potenza, una leva può essere classificata in:
- leva di secondo genere;
In questa sezione studieremo le leve di secondo genere.
Definizione di leva di secondo genere
Una leva si dice di secondo genere se la forza resistente si trova tra il fulcro e la forza motrice (potenza):
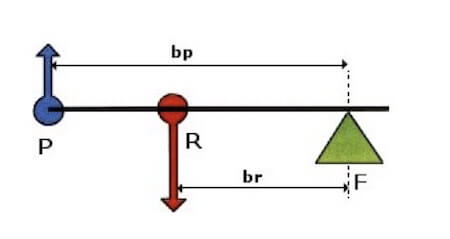
Guadagno di una leva di secondo genere
Si definisce guadagno di una leva il rapporto tra la forza resistente e la forza motrice:
G = R/P
Dalla equazione:
P ∙ bp = R ∙ br
che rappresenta la condizione di equilibrio di una leva, si ha che:
R / P = bp / br
Pertanto il guadagno di una leva si può esprimere anche in funzione dei bracci:
G = bp / br
Poiché in una leva di secondo genere il braccio della potenza è sempre superiore al braccio della forza resistente allora il guadagno sarà sempre superiore all'unità, per cui una leva di secondo genere risulterà sempre vantaggiosa.
Esempi di leve di secondo genere
Un esempio di leva di secondo genere è lo schiaccianoci:
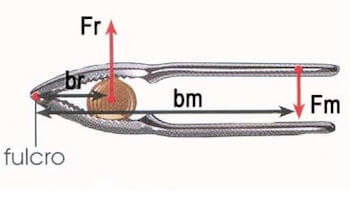
Nella figura sopra possiamo osservare come il braccio della forza motrice è rappresentato dall'intera lunghezza dello schiaccianoci, mentre la noce rappresenta la forza resistente.
Il fulcro è il perno dello schiaccianoci.
Un altro esempio di leva di secondo genere è la carriola:
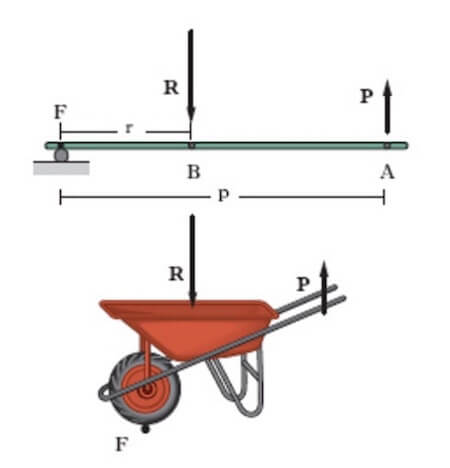
Esercizio
Una leva di secondo genere è lunga 120 cm e la resistenza è caratterizzata da una massa di 21 kg.
Calcolare quale deve essere la potenza da applicare se il braccio della resistenza è ⅓ di quello della potenza.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sul calcolo della potenza di una leva.
Esercizi sulle leve
Li trovi qui: esercizi sulle leve.
Link correlati:
Quali sono alcuni esempi di leve di primo genere?
Quali sono alcuni esempi di leve di terzo genere?
Studia con noi