Leggi di Newton
Definizione delle leggi di Newton
La dinamica è quella branca della fisica (ed in particolare della meccanica) che si occupa di studiare il moto dei corpi e delle sue cause.
Un importante contributo allo studio della dinamica fu dato dal fisico inglese Isaac Newton mediante le sue tre leggi (noti anche come principi di Newton o principi della dinamica).
Il primo principio della dinamica (o principio di inerzia o prima legge di Newton) stabilisce che un corpo non soggetto a forze o soggetto a forze la cui risultante è nulla, permane nel suo stato di quiete o continua a muoversi di moto rettilineo uniforme.
Il secondo principio della dinamica (o legge fondamentale della dinamica o seconda legge di Newton) afferma che la somma di tutte le forze che agiscono su un corpo è uguale al prodotto della massa per l'accelerazione del corpo:
∑F = m ∙ a
Il terzo principio della dinamica (o principio di azione e reazione o terza legge di Newton) afferma che ad ogni azione corrisponde una reazione uguale e contraria.
Si rimanda alle singole voci per ulteriori approfondimenti.
Applicazioni delle leggi di Newton
Le leggi di Newton possono essere utilizzate sostanzialmente per determinare:
- accelerazione, velocità e posizione di un corpo in funzione del tempo, note tutte le forze che agiscono su di esso;
- le forze che agiscono sul corpo, note l'accelerazione, la velocità e la posizione in funzione del tempo di un corpo.
Utilizzeremo dunque la seconda legge di Newton:
∑F = m ∙ a
studiando le strategie risolutive comuni a tutti i tipi di problemi ed applicandola a queste situazioni, che sono le più comuni che si possono riscontare nello studio della fisica classica:
- moto rettilineo con forze costanti
- moto circolare.
Moto rettilineo con forze costanti
Le principali tipologie di forze presenti in questo tipo di situazioni sono la forza peso P sempre rivolta lungo la verticale verso il basso, la forza di reazione N che il piano su cui poggia il corpo esercita su di esso, forze di tensione T se sono presenti funi, forza di attrito Fa se consideriamo superficie scabre.
Quando si deve risolvere un problema di dinamica relativo ad un moto rettilineo con forze costanti è bene seguire la seguente scaletta:
- scegliere un sistema di riferimento (assi coordinati) adeguato alla situazione descritta;
- isolare il corpo e disegnare il diagramma di corpo libero rappresentando le forze come vettori con il corretto verso e la corretta direzione, facendo attenzione ad indicare bene gli angoli se i piani sono inclinati;
- applicare la seconda legge di Newton ∑F = m ∙ a per ogni asse coordinato;
- risolvere le equazioni che derivano dal punto 3 per calcolare o la forza incognita o l'accelerazione;
- infine analizzare il risultato ottenuto cercando di capire se il dato ricavato è coerente con la schematizzazione del problema e cercare di analizzare il dato (se espresso solo in funzione dei parametri, senza numeri) al variare delle incognite nei casi limite.
Esercizio
Calcolare l'accelerazione con cui scende un blocco di massa m lasciato libero di muoversi su di un piano inclinato di un angolo θ rispetto all'orizzontale.
Lo svolgimento dell'esercizio lo trovi qui: accelerazione lungo un piano inclinato.
Moto circolare
Consideriamo un corpo di massa m che si sta muovendo lungo una traiettoria circolare di raggio r con velocità costante v.
Allora su quel corpo agirà un'accelerazione centripeta di modulo pari a v2/r e diretta verso il centro della circonferenza.
La presenza di questa accelerazione è dovuta al fatto che la velocità cambia in continuazione la propria direzione lungo il percorso circolare, ed ogni vettore velocità è tangente alla traiettoria:
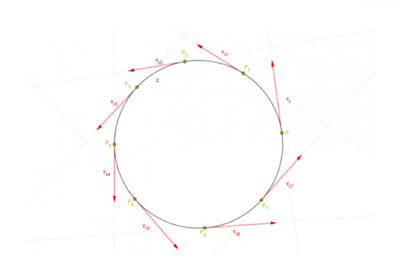
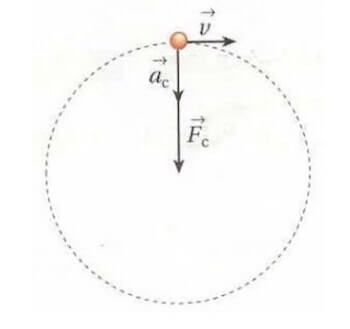
Visto che è presenta l'accelerazione centripeta allora sarà sicuramente attiva pure una forza, detta forza centripeta di modulo pari al prodotto della massa m del corpo per l'accelerazione centripeta e di direzione e verso pari a quella dell'accelerazione.
Esercizio
Una sfera di massa m è posta in rotazione lungo una circonferenza verticale da una corda di lunghezza L.
La velocità della sfera vale Vb nel punto più basso della traiettoria mentre vale Va in quello più in alto.
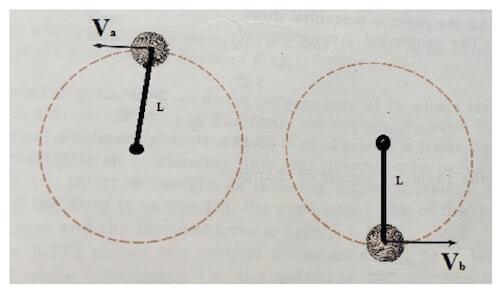
Determinare la tensione della corda nei due punti.
Lo svolgimento dell'esercizio lo trovi qui: sfera in rotazione lungo una circonferenza verticale.
Link correlati:
Che cosa sono le macchine semplici?
Studia con noi