Grandezze vettoriali
Che cosa sono le grandezze vettoriali?
In fisica alcune grandezze sono individuate oltre che dal valore numerico anche da direzione e verso.
Tali grandezze si dicono vettoriali.
Esempi di grandezze vettoriali sono lo spostamento, la velocità, l'accelerazione, la forza, ecc.
Ogni grandezza vettoriale è rappresentata da un vettore; a sua volta ogni vettore è individuato da un punto di applicazione in cui la grandezza vettoriale ha origine ed è tracciato come una freccia orientata avente lunghezza pari al suo modulo.
Come si indica una grandezza vettoriale
Un vettore si indica con una lettera sormontata da una freccia: 
, 
, oppure utilizzando gli estremi del segmento 
, in cui A è il punto di applicazione.
Modulo, direzione e verso di un vettore
Si definisce modulo di un vettore e si indica con |a| la misura del vettore stesso.
Ad esempio: una velocità |v| di 5 m/s, accelerazione |a| di 9,8 m/s2, una forza |F| di 6 N.
Il modulo corrisponde con la lunghezza del vettore.
La direzione di un vettore è la retta su cui esso giace: ad esempio un vettore giacente lungo l'asse x, un vettore lungo la retta inclinata di 45° rispetto all'orizzontale, etc.
Il verso rappresenta invece l'orientazione del vettore lungo la sua retta direzione: ad esempio per un vettore giacente lungo l'asse x il verso sarà rivolto o verso destra o verso sinistra.
Operazioni con i vettori
Le operazioni consentite tra vettori sono la somma vettoriale, determinabile tramite il metodo punta coda, la differenza tra due vettori, sempre applicando lo stesso metodo; vi sono inoltre due tipi di prodotti e di rapporti.
Esiste infatti la possibilità di moltiplicare o dividere un vettore per un numero (scalare).
In particolare il prodotto di un vettore per uno scalare m corrisponde ad un vettore che ha stessa direzione e verso di (verso opposto solo se m < 0) e modulo pari a |a| ∙ m.
Allo stesso modo il rapporto tra un vettore ed uno scalare m è ancora un vettore con stessa e direzione e verso di quello originario ma modulo pari a |a|/m.
Il prodotto di due vettori può essere invece di tipo scalare o vettoriale (si parlerà quindi di prodotto scalare e di prodotto vettoriale).
In particolare il prodotto scalare restituisce un numero scalare mentre il risultato di un prodotto vettoriale è ancora un vettore.
Componenti di un vettore
In generale, posto un vettore 
nel piano e scelto un opportuno sistema di riferimento cartesiano, si possono individuare le due componenti x e y del vettore; si indicheranno con 
e 
le due proiezioni del segmento orientato lungo i due assi.
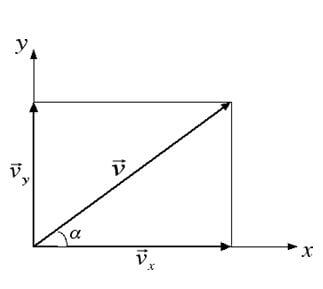
Come possiamo notare in figura, il vettore risulta inclinato di un angolo α rispetto all'orizzontale e per questo motivo i moduli delle due componenti x e y risultano per ragioni di trigonometria:
|Vx| = |V| ∙ cosα
e
|Vy| = |V| ∙ senα
Applicando il teorema di Pitagora vale la relazione:
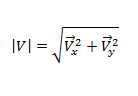
Oltre alle grandezze vettorili esistono anche le grandezze scalari; queste ultime sono grandezze che possono essere descritte soltanto con un numero.
Esercizio sulla scomposizione di un vettore
Un aeroplano si sta muovendo lungo una direzione di 22° Nord - Est.
Trovare le componenti del suo spostamento quando avrà percorso 215 km.
La soluzione la trovi qui: esercizio sulla scomposizione di un vettore.
Link correlati:
Quali sono alcuni esempi di grandezze vettoriali?
Qual è la differenza tra le grandezze scalari e le grandezze vettoriali?
La pressione è una grandezza scalare o vettoriale?
Quali sono alcuni esempi di grandezze scalari?
Studia con noi