Corpo rigido
Cos'è un corpo rigido?
Il corpo rigido è un sistema di punti materiali in cui le distanze tra tutte le possibili coppie di punti non possono variare.
Esempi di corpo rigido possono essere una sfera da biliardo, una ruota, una trottola, ecc.
Moto di un corpo rigido e centro di massa
Quando si studia il moto di un corpo rigido ci si rende conto che i vari punti possono descrivere traiettorie diverse.
Osserviamo la figura sotto che descrive il moto di rotolamento di una sfera rigida.
Individuati tre punti fissi sulla sfera, Q, P ed O, si nota che quando la sfera rotola verso destra la traiettoria seguita dai tre punti è molto diversa.
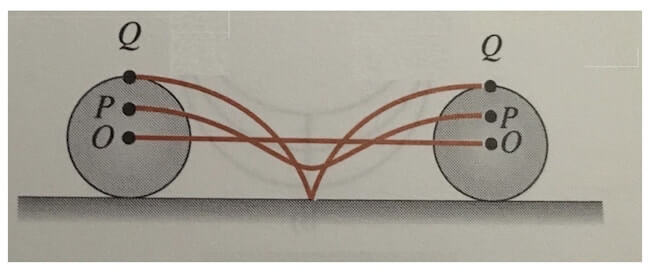
Notiamo però che la traiettoria seguita dal centro della sfera O è una linea retta.
Questo spostamento riassume lo spostamento di tutti gli altri punti ed in fisica per semplificare lo studio del moto di un corpo rigido si ci riferisce dunque al moto del centro di massa (baricentro) del sistema di punti.
Il centro di massa, per un corpo omogeneo e simmetrico, coincide col centro di simmetria: ad esempio per una sfera è il suo centro.
In generale la posizione del centro di massa è la media pesata delle posizioni delle singole masse mi che compongono il corpo rigido moltiplicate per la distanza x da un polo fisso e diviso per la massa totale M del corpo:
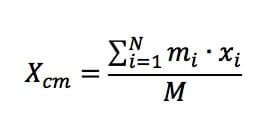
Pertanto per studiare il moto globale di un corpo rigido, se ne studia il moto del suo centro di massa.
Moto di traslazione del corpo rigido
Nel moto di traslazione di un corpo rigido tutti i punti descrivono traiettorie uguali, in generale curvilinee, e percorrono tutti tale traiettoria con la stessa velocità in modulo direzione e verso.
Il vettore velocità può variare nel tempo, ma la velocità di ogni punto corrisponde con quella del centro di massa:
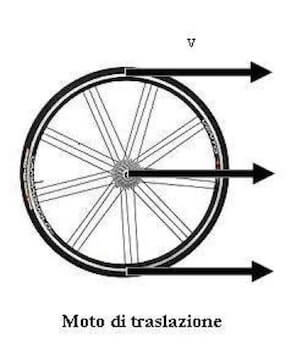
Riferendoci a velocità del centro di massa Vcm ed accelerazione del centro di massa acm le grandezze significative in una traslazione sono:
- quantità di moto: P = m ∙ Vcm
- energia cinetica: Ek = ½ ∙m∙Vcm2
- forza: Ftot = m ∙ acm
- momento angolare: L = Lcm = rcm x m ∙ Vcm
Moto di rotazione del corpo rigido
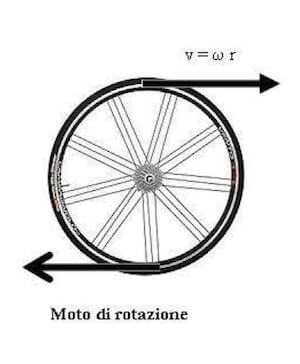
Nel moto di rotazione di un corpo rigido tutti i punti descrivono un moto circolare uniforme; per cui in un dato istante tutti i punti avranno la stessa velocità angolare ω parallela all'asse di rotazione, mentre le velocità dei singoli punti i sono diverse in base alla distanza Ri dall'asse di rotazione, in modulo:
Vi = ω∙Ri
L'equazione del moto risulta:
M = dL/dt
in cui M è il momento totale delle forze ed L il momento angolare entrambi calcolati rispetto allo stesso polo.
Momento angolare nel corpo rigido
Consideriamo la rotazione di un corpo rigido attorno ad un asse fisso.
Poiché i punti dell'asse di rotazione sono punti fissi, possono essere utilizzati come poli per il calcolo dei momenti.
Il vettore velocità angolare ω ha direzione fissa e coincidente con l'asse di rotazione.
Se ω varia allora saremo in presenza di un'accelerazione angolare α dato dal rapporto tra la variazione della velocità angolare e il tempo:
α = dω/dt
in cui il simbolo di delta è sostituito dal simbolo di differenziale d per considerare anche variazioni infinitesimali della velocità angolare.
La proiezione del momento angolare L sull'asse di rotazione è dato da:
L = I ∙ ω
in cui I è il momento di inerzia del corpo rispetto all'asse di rotazione.
Le formule per il calcolo del momento d'inerzia delle principali forme di corpo rigido sono riportate nella seguente tabella:
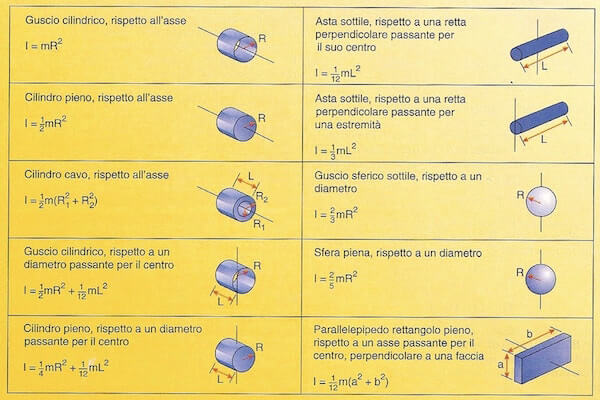
Mentre per un anello sottile, disco omogeneo o anello con spessore, la tabella dei momenti di inerzia è la seguente:
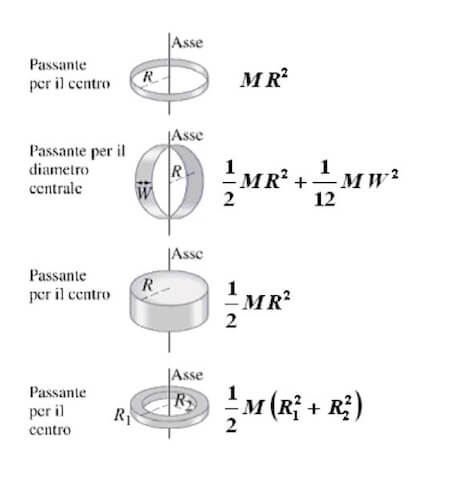
Equazione del moto di un corpo rigido
Nel caso più semplice di momento angolare L parallelo a ω l'equazione del moto di rotazione di un corpo rigido è:
M = I ∙ α
Ovvero il momento risultante delle forze esterne è pari al prodotto del momento di inerzia per l'accelerazione angolare.
Se il momento risultante delle forze esterne rispetto a un punto qualsiasi risulta nullo allora siamo in presenza della condizione di equilibrio per un corpo rigido.
Energia cinetica e lavoro
L'energia cinetica rotazionale di un corpo rigido è pari a:
Ek = ½ ∙ I ∙ ω2
L'energia cinetica dunque dipende dal momento di inerzia del corpo rispetto all'asse di rotazione.
Il lavoro invece si trova come:
L = ΔEk = ½ ∙ I ∙ (ωfin2 – ωini2)
Esercizio
Un disco omogeneo inizialmente fermo, viene posto in rotazione fino a fargli compiere 150 giri in un minuto.
Sapendo che il diametro del disco è 80 cm e la sua massa 100 kg, calcolare il lavoro necessario per la rotazione.
Lo svolgimento dell'esercizio lo trovi qui: rotazione di un corpo rigido.
Link correlati:
Che cosa si intende con nutazione?
Studia con noi